Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Частица в ящике с непроницаемыми стенками
|
|
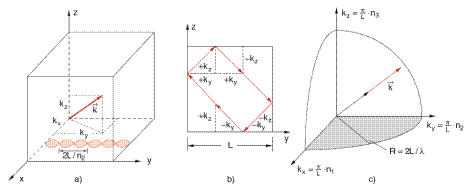
Рассмотрим в рамках квантовой механики движение частицы, заключенной в некотором ограниченном объеме V. Пусть этот объем имеет форму прямоугольного параллелепипеда (рис. 20.11). Построим прямоугольную декартову систему координат так, чтобы плоскости, ограничивающие движение частицы, имели уравнения: х = 0, х = а, у = 0, у = b, z = 0 и z= с, где а, b и с - длины ребер параллелепипеда.
Если частица испытывает воздействие только со стороны стенок "ящика" при ударах о них, а внутри него движется свободно, то зависимость
Ее потенциальной энергии от координат можно описать формулой
 |
0 при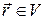 
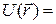∞ при
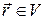
где V - область пространства внутри ящика.
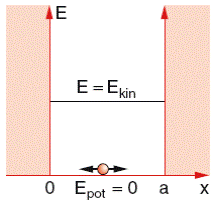
Рис.20.11. Частица в ящике с непроницаемыми стенками
По условиям задачи волновая функция вне ящика всюду равна нулю. Функцию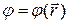 
, которая описывает стационарное движение частицы внутри ящика, где U= 0, найдем из уравнения Шредингера (4.43)
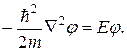
Так как волновая функция должна быть непрерывной по определению, на стенках ящика она должна быть равна нулю:
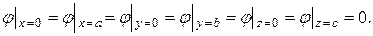
Имея в виду, что стационарные состояния частицы в одномерной потенциальной яме описываются функцией (20.50), предположим, что
стационарные состояния частицы в прямоугольном ящике описываются
функцией
φ (x,y,z) = A sin k 1 x sin k 2 y sin k 3 z, (20.61)
где
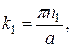
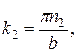
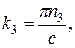(20б2)
n 1, n 2, n 3 = 1, 2, 3,…
Заметим, что совокупность чисел n 1, n 2, n 3 можно рассматривать как трехзначный номер волновой функции:
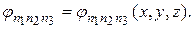
В самом деле, нетрудно видеть, что функция (20.61) удовлетворяет граничным условиям (20.60). Подстановка этой функции в стационарное уравнение Шредингера (20.59) убеждает в том, что она является его решением, если энергия частицы Е связана с квантовыми числами n 1, n 2, n 3 формулой
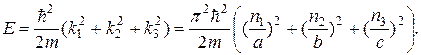
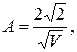
Величины k 1, k 2 и k 3 можно рассматривать как проекции на оси координат волнового вектора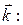 
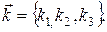(20.64)
При этом энергию частицы можно представить формулой
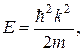
где к - модуль волнового вектора к.
Постоянную А в формуле (20.61) нетрудно найти из условия нормировки (19.28) волновой функции:
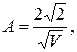
где V = abc - объем параллелепипеда.
Итак, доказано, что возможные стационарные состояния частицы в ящике, описываемые функциями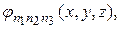 
образуют счетное множество; а соответствующие этим состояниям значения энергии частицы составляют дискретный спектр.
Date: 2015-05-19; view: 902; Нарушение авторских прав