Свободная частица

Движение частицы называется свободным, когда на нее не действуют внешние силы. В таком случае саму частицу также называют свободной. Потенциальную энергию свободной частицы можно считать равной нулю: U ≡ 0.

Волновая функция 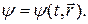, описывающая движение свободной ча­стицы удовлетворяет уравнению Шредингера (4.33). Рассмотрим поток свободных частиц, движущихся вдоль оси х. Движение частиц в этом случае описывается волновой функцией

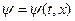, (20.1)

которая зависит только от одной координаты х и удовлетворяет уравне­нию Шредингера (4.32)

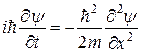(20.2)

Волновая функция, описывающая стационарное движение частиц, по определению (4.26) будет

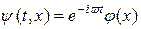(20.3)

Подстановка этой функции в уравнение (20.2) приводит к стационарному уравнению Шредингера

(20.4)

Где

E = ћω (20.5)

Введем обозначение

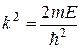(20.)

и запишем уравнение (20.4) так:

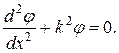. (20.6)

Общее решение этого уравнения можно представить в виде

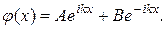
При этом волновая функция (20.3) будет иметь вид

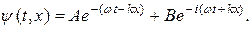
Первое слагаемое в этой формуле

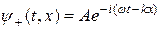(20.8)

есть гармоническая волна, бегущая вдоль оси х в сторону возрастания координаты, а второе

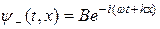
- волна, бегущая в противоположном направлении. Комплексные коэф­фициенты А и В называются амплитудами бегущих волн. Эти функции описывают потоки частиц, летящих вдоль оси х навстречу друг другу.

Подействуем на функцию Ψ₊ оператором импульса 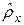р_Х) т.е. вычислим функцию 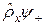р_хф+-

Используя определение (4.19), найдем, что

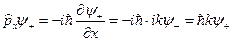
или

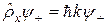
Из этого равенства следует, что функция Ψ₊ является собственной функ­цией оператора импульса р_х, а соответствующее собственное значение равно hk. На основании теоремы, доказанной в предыдущем разделе, можно утверждать, что в состоянии, описываемом волновой функцией Ψ₊ , частица обладает импульсом р_х, который в точности равен собствен­ному значению ћk:

р_x=ћk.

Таким образом, мы пришли к соотношению, которое вместе с формулой (20.5) составляет соотношения де Бройля (19.2).

Функции (20.7) - (20.9) таковы, что интеграл

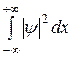
от квадрата модуля волновой функции расходится и не может быть ра­вен единице. Поэтому в этом случае считают, что величина 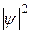есть концентрация п частиц в потоке, а не плотность вероятности. С учетом зависимости (20.3) придем к формуле

n(x) = | φ (x)‌‌|²

Date: 2015-05-19; view: 553; Нарушение авторских прав