Гармонический осциллятор

Исследуем движение частицы, на которую действует сила F_x = - cx, где с - положительная постоянная.

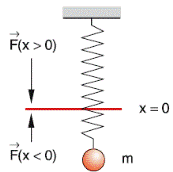
Модель классического осцилятора

В классической механике движение частицы описывается посредством функции х = x(t), удовлетворяющей уравнению Ньютона

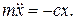
Это уравнение удобно привести к виду

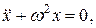(20.37)

где

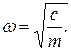. (20.38)

Решением дифференциального уравнения (20.37) является функция

x (t) = A cos (ωt + β),

которая описывает гармонические колебания с частотой ω. Частицу, со­вершающую такое движение, называют гармоническим осциллятором.

Когда частица находится в силовом поле F_x = - cx, она обладает потенциальной энергией

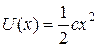(20.39)

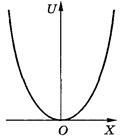
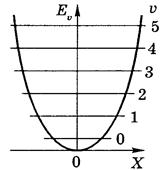
Графиком этой функции является парабола, ветви которой направлены вверх (рис. 20.6). Такой график также называется потенциальной ямой.

В квантовой механике стационарные состояния гармонического осцил­лятора описывают посредством функции φ =φ (x),; которая удовлетво­ряет уравнению Шредингера

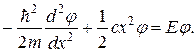(20.40)

Это уравнение имеет счетное множество решений φ_n = φ_n (x), где число п = 0, 1, 2, 3,... называют колебательным квантовым числом. Спектр энергий гармонического осциллятора определяется формулой

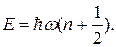
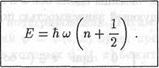
Рис. 20.6. Параболическая потенциальная яма

Задача. Основное состояние квантового гармонического осциллятора описывается функцией

φ (x)= A exp(- ax²), (20.42)

где А и а - положительные постоянные. При помощи уравнения Шре­дингера (20.40) найти постоянную а и энергию частицы в этом состоянии. Используя условие нормировки, найти постоянную А.

Указание. В вычислениях использовать формулу Пуассона

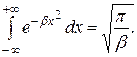
Date: 2015-05-19; view: 652; Нарушение авторских прав