Частица в потенциальной яме с бесконечно высокими стенками

Предположим, что при движении вдоль оси х частица встречает на своем пути две непреодолимые преграды, которые расположены в точ­ках х = 0 и х = l (рис. 20.3). В пространстве между этими преградами, т.е. при x 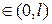, частица движется свободно. Сталкиваясь с одной из преград, она отражается от нее и изменяет направление своего движе­ния на противоположное. По этой причине частица не может выйти за пределы интервала (0, l).

В таком случае зависимость потенциальной энергии частицы от координаты х имеет вид

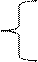0 при x 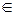(0,1),

U (x) =

∞ при x 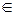(0,1). (20.28)

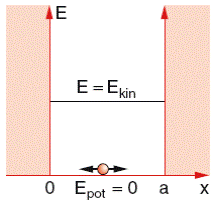
Рис. 20.3. Частица между непроницаемыми стенками 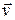l x

График зависимости (20.28) представлен на рис. 20.4. Эта кривая также называется потенциальной ямой. В данном случае потенциальная яма имеет бесконечно высокие вертикальные стенки.

U = ∞ U = 0 U = ∞

Рис. 20.4. Прямоугольная потенциальная яма с бесконечно высокими стенками

Так как при x 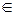(0, l), потенциальная энергия U(x) равна нулю, урав­нение Шредингера (20.23) для этих значений х принимает вид

φ ^// + k²φ = 0 при x 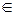(0, l), (20.29)

где

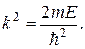(20.30

Запишем решение уравнения (20.29) в виде

φ (x) = A sin (kx + a),

где А и а - постоянные интегрирования, для отыскания которых необхо­димо сформулировать граничные условия, т.е. найти значения функции φ (x) при х = 0 и x = 1. Так как частица не может оказаться вне ин­тервала (0, l), волновая функция должна быть равна нулю вне этого интервала и в точках 0 и l:

φ (0) = 0, φ (l) = 0. (20.32)

Применим эти условия к функции (20.31). Получим равенства

A sin а = 0, A sin (kl + a) = 0. (20.33)

Амплитуда А не может быть равна нулю, так как это означало бы, что равна нулю вероятность найти частицу в интервале (0, l), т.е. что она просто не существует. Поэтому положим

a = 0

При этом первое из равенств (20.33) выполняется, а второе принимает вид

sin kl = 0.

Отсюда следует, что

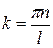, (20.34)

где п - целое число.

n = 1, 2, 3,…

а = 0.

Итак, волновая функция, описывающая стационарное состояние ча­стицы в потенциальной яме (20.28), имеет вид

φ (x) = A sin 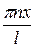. (20.35)

Согласно вероятностной трактовке квантовой механики физический смысл имеет не сама волновая функция, а квадрат ее модуля. Поэтому волно­вые функции, модули которых тождественно равны друг другу, в дей­ствительности описывают одно и то же состояние частицы. Учитывая это, удобно считать, что в формуле (20.35) квантовое число п принимает только целые положительные значения:

n = 1,2,3,...

В противном случае волновые функции, описывающие одно и то же со­стояние частицы, соответствовали бы различным квантовым числам, что сопряжено с некоторыми неудобствами при подсчете числа возможных стационарных состояний частицы.

Функцию (20.35) можно записать так:

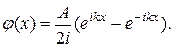
При этом волновая функция (20.21) будет представлять собой суперпо­зицию двух бегущих навстречу друг другу волн одинаковых амплитуд:

.

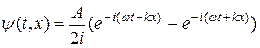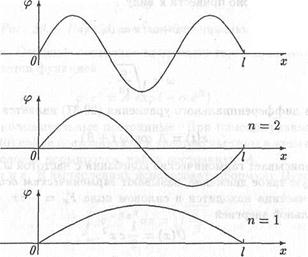
Таким образом, функция (20.35) есть стоячая волна, образованная в ре­зультате интерференции двух бегущих волн. Графики функции (20.35) для значений квантового числа п = 1, 2 и 3 изображены на рис. 20.5.

Используя соотношение (20.30), связывающее энергию частицы и вол­новое число, получим формулу

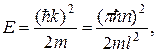(20.36)

которая описывает энергетический спектр частицы. Наиболее важный вывод, который следует сделать из рассмотренного примера, заключа­ется в следующем. Энергия частицы, которая совершает стационарное движение внутри потенциальной ямы, "квантуется", т.е. может прини­мать не любые, а только вполне определенные дискретные значения

Используя условие нормировки, найдем постоянную А в формуле (20.35). Для этого подставим функцию в равенство (20.25). Получим:

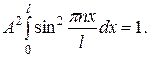
Так как интеграл

,

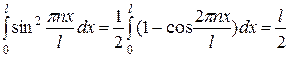будем иметь

.

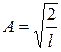п = 3

Рис. 20.5. Волновая функция φ = φ (x) для ямы с бесконечными стенками

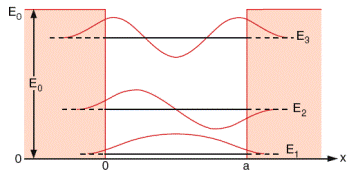
Уровни энергии и собственные функции для частицы в яме с конечными стенками

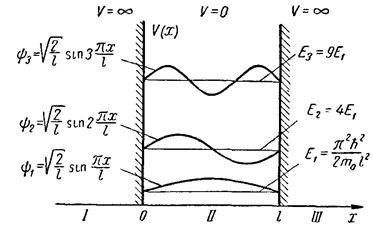
Частица в яме с бесконечными стенками соколов и др стр 82

Date: 2015-05-19; view: 1370; Нарушение авторских прав