Уравнение Шредингера

Основным законом в квантовой механике является уравнение для вол­новой функции

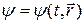
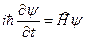, (19.29)

В 1926 г. австрийский физик Эрвин Шредингер, развивая идеи де Брой-ля о волновых свойствах потоков частиц вещества, первым записал это уравнение (Нобелевская премия 1933 г.). Уравнение Шредингера имеет в квантовой механике такое же фундаментальное значение, какое имеет второй закон Ньютона в классической механике.

С учетом строения оператора Гамильтона (19.24) уравнение Шредин­гера можно преобразовать к виду

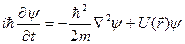. (19.30)

Это есть дифференциальное уравнение в частных производных. Для то­го чтобы среди множества различных решений уравнения Шредингера найти единственное 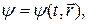необходимо выделить его при помощи какого-либо дополнительного условия. В качестве такого условия обыч­но выбирают начальное условие

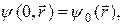
где 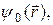- известная функция. Это условие задает зависимость ψ от 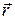при t = 0. Кроме этого, волновая функция в любой момент време­ни должна удовлетворять условию нормировки (19.17). Зная функцию 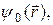определяющую состояние частицы в начальный момент времени t = 0, из уравнения Шредингера можно найти функцию 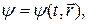опи­сывающую состояние частицы в любой другой, более поздний момент времени t > 0.

Рассмотрим, как можно получить уравнение Шредингера из предполо­жения, что волна де Бройля (19.5) является решением этого уравнения. Волна де Бройля (19.5) описывает поток свободно летящих частиц, ка­ждая из которых имеет энергию Е и импульс р. Аргументами волновой функции ψ в данном случае служат время t и координата х. При этом энергию Е и импульс р частицы следует рассматривать как параметры. Естественно предположить, что волна де Бройля есть частное решение некоторого уравнения, которое выражает общий закон, определяющий движение частиц в рамках квантовой механики. В таком случае это уравнение не должно содержать в себе параметров, характеризующих какой-то один вид движения частицы. Исходя из этого предположения, найдем дифференциальное уравнение, частным решением которого явля­ется волна де Бройля (19.4), или (19.5). При этом будем иметь в виду, что энергия свободной частицы Е и ее импульс р связаны соотношением

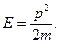(19.31)

Найдем первую производную от функции (19.4) по t и вторую по х:

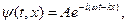(19.4)

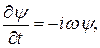
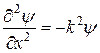
При помощи формул де Бройля (19.3) эти равенства можно записать так:

k = .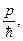

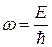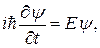
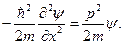
Из этих равенств нетрудно исключить параметры Е и р. Правые части этих равенств совпадают в силу соотношения (19.31). Следовательно, должны быть равны их левые части. Таким образом, приходим к урав­нению

В общем случае волновая функция свободной частицы может зависеть от всех координат: х, у и z. Очевидно, что в этом случае она должна удовлетворять уравнению

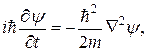(19.33)

которое, с учетом обозначения (19.21) оператора 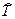кинетической энергии, можно записать так:

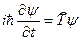. (19.34)

Это уравнение для свободной частицы нетрудно обобщить на случай, ко­гда частица движется в консервативном силовом поле. В этом случае ее полная энергия будет равна сумме кинетической и потенциальной энер­гий. Полной энергии частицы в квантовой механике соответствует опе­ратор 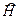, определяемый формулой (19.23). Таким образом, более общее уравнение для волновой функции получим, если заменим в уравнении (19.34) оператор кинетической энергии 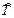на оператор полной энергии 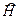. В результате придем к уравнению Шредингера (19.29). Строго говоря, приведенные преобразования не являются выводом уравнения Шредин­гера, но они помогают понять его происхождение и физическое содержа­ние.

Date: 2015-05-19; view: 581; Нарушение авторских прав