Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Операторы в квантовой механике. При вычислении средних значений различных физических величин в квантовой механике поступают следующим образом
|
|
При вычислении средних значений различных физических величин в квантовой механике поступают следующим образом. Каждой физической величине а ставится в соответствие оператор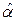 
, -> a^ который символизирует совокупность математических операций, производимых над волновой функцией 
. Результатом этих операций является другая функция 
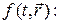
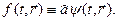
Координате х частицы соответствует оператор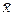 
, который по определению равен х:
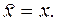(19.18)
Таким образом, действие оператора 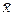на волновую функцию
в данном случае сводится к ее умножению на x. В результате получим функцию
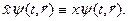
Оператор импульса 
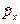определяется так:
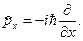(19.19)
Из этого определения следует, что
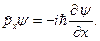
т.е. действие оператора 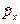на функцию ψ состоит в дифференцировании функции по х и умножении на -iћ.
Согласно определению (19.19) оператор 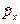импульса частицы можно записать как
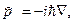(19.20)
где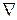 
- дифференциальный оператор "набла" такой, что
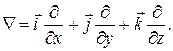
Оператор кинетической энергии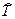 
связан с оператором импульса 
так же, как кинетическая энергия частицы Т связана с ее импульсом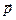 
:
= 
= 
,
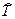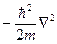где
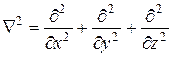
- оператор Лапласа.
Оператор потенциальной энергии равен самой потенциальной энергии: (19.21)
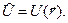(19.22)
Оператор полной энергии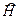 
называется оператором Гамильтона, или гамильтонианом. Этот оператор равен сумме операторов кинетической и потенциальной энергий:
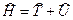. (19.23)
Более подробно это символическое равенство можно записать так:
= 
,
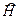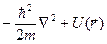Физический смысл какого-либо оператора а в квантовой механике заключается в том, что с его помощью по формуле
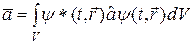(19.25)
можно вычислить среднее значение величины а. В общем случае среднее значение изменяется с течением времени: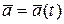 
. В частном случае, когда средние значения всех физических величин, характеризующих движение микрочастицы, не зависят от времени, состояние частицы называется стационарным. Такое состояние описывается волновой функцией вида
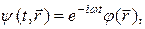(19.26)
где ω - постоянная, а функция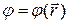 
зависит только от радиус-вектора 
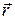. Так как комплексно сопряженная функция
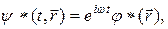
подстановка функции (19.26) в формулу (19.25) дает среднее значение
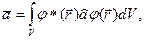(19.27)
которое не изменяется с течением времени.
Подстановка функции (19.26) в условие нормировки (19.17) приводит
к равенству
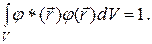(19.28)
Date: 2015-05-19; view: 991; Нарушение авторских прав