Давление света. Опыты Лебедева

Максвелл на основе созданной им теории электромагнитного поля предсказал, что падающая на поверхность какого-либо тела электромаг­нитная волна должна оказывать на него давление, величина которого пропорциональна потоку энергии волны. Эта величина очень мала и для ее измерения необходимы очень точные приборы.

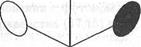
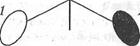
Рис. 17.9. Схема опыта Лебедева по измерению давления света

В 1899 г. русский физик-экспериментатор Петр Николаевич Лебедев (1866 - 1912) осуществил опыты по измерению давления света. Схема опыта Лебедева показана на рис. 17.9. Световая волна падает на спе­циальную конструкцию, основными элементами которой являются лег­кие "крылышки" 1 - 4- Одна сторона каждого крылышка зачернена, а другая представляет собой маленькое зеркало. Конструкция подвеше­на на нити 5 и помещена в стеклянный сосуд, из которого откачивается воздух. Свет оказывает различное давление на зачерненную и зеркаль­ную поверхности крылышек. В результате момент сил, действующих на конструкцию, не равен нулю. При этом она поворачивается. Нить закручивается и в ней возникают упругие силы, которые противодей­ствуют силам светового давления. Когда конструкция, отклонившись от

начального положения, придет в состояние покоя, момент упругих сил будет равен моменту сил светового давления. Так как момент упругих сил прямо пропорционален углу поворота конструкции, по углу поворо­та можно определить значение светового давления. Энергия падающего света измерялась при помощи термоэлемента. Как показали измерения, световое давление прямо пропорционально энергии света, падающего за единицу времени на единицу площади освещаемой поверхности. Изме­ренное Лебедевым значение светового давления в пределах ошибок из­мерений совпало со значением, вычисленным Максвеллом. Таким обра­зом, Лебедев экспериментально доказал существование предсказанного Максвеллом давления света.

Опыты Лебедева в свое время рассматривались как одно из главных подтверждений справедливости созданной Максвеллом теории электро­магнитного поля. Давление света можно вычислить также на основе представлений о свете как совокупности частиц.

17.6. Давление пучка света

Будем рассматривать электромагнитное излучение как поток фото­нов. При столкновении с поверхностью тела фотон передает ему им­пульс. Следствием многочисленных столкновений фотонов с поверхно­стью является давление, оказываемое электромагнитным излучением на эту поверхность.

Пусть плоская электромагнитная волна интенсивности I падает на плоскую поверхность под углом θ к нормали. Коэффициент отражения света поверхностью равен ρ. Найдем при помощи корпускулярных пред­ставлений нормальное давление, оказываемое светом на поверхность. В таком случае плоскую электромагнитную волну следует рассматривать как однородный поток фотонов, падающих на поверхность под углом θ. Предположим, что все эти фотоны имеют одну и ту же энергию ε. При этом импульс каждого из них будет равен

p=ε/c (17.20)

Для того чтобы найти давление Р на поверхность необходимо вычи­слить или измерить силу F_╨., которая действует на нее по направлению нормали к ней, а затем разделить эту силу на площадь поверхности S:

Р = F_╨/S. (17.21)

Сила, действующая на поверхность со стороны излучения, согласно за­кону изменения импульса равна отношению приращения импульса ∆p_s, полученного поверхностью от фотонов, ко времени τ за которое это при­ращение произошло:

F_╨ = ∆p_s/τ (17.22)

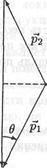
Приращение импульса ∆p_s поверхности равно сумме импульсов, кото­рые она приобретает после многочисленных ударов о нее фотонов. Пусть p₁ - импульс фотона, подлетающего к поверхности, а р₂ - импульс отраженного фотона (рис. 17.10).

p_Somp

Рис. 17. 10. Удар фотона о поверхность и отражение от нее

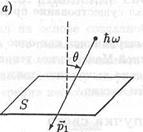
Рис. 17.11. К закону сохранения импульса фотона и поверхности.

После отражения фотона поверхность получает импульс p_soтp, который направлен по нормали к ней

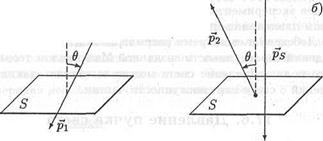
Рис.17. 10. Удар фотона о поверхность и отражение от нее

Закон сохранения импульса системы, состоящей из фотона и поверхности, выражается равенством

P₁=P₂+ P_Sotr (17.23)

где P_Sotr - импульс, приобретенный поверхностью после отражения фо­тона. Будем считать поверхность совершенно гладкой. В этом случае угол отражения света будет равен углу падения θ. Импульсы фотона и поверхности, удовлетворяющие равенству (17.23), показаны на рис. 17.11. При отражении фотона от поверхности его энергия не изменя­ется. Не изменяется также и модуль его импульса: p₁ = р₂. Из рис. 17.11 нетрудно найти модуль вектора p_Somp

Если импульс р₁ падающего фотона направлен под углом θ к нормали, то после отражения фотона поверхность получит импульс

p_Somp = 2ε cosθ /c (17.24)

Если фотон поглощается поверхностью, то закон сохранения импульса будет иметь вид

P₁= p_Sпoгя, (17.25)

т.е. поверхность получит импульс р₁ поглощенного ею фотона. При этом проекция полученного поверхностью импульса на нормаль к ней будет

p_Sпогл = ε cosθ /c (17.26)

Пусть за время τ на поверхность падают N фотонов. Энергии W_nad излучения, падающего за это время на поверхность, будет равна произ­ведению энергии ε одного фотона на их число:

W_nad = εN., (17.27)

Таким же образом связаны энергия W_omp излучения, отраженного по­верхностью за это время, и число N_omp отраженных фотонов:

W_omp = εN_omp

Коэффициент отражения σ есть отношение энергии W_omp отраженного поверхностью излучения к энергии W_nad излучения, падающего на нее:

σ = W_отр/ W_nad (17.29)

Подставим в это равенство выражения (17.27) и (17.28). Получим

N_omp = σN (17.30)

Так как число поглощенных поверхностью

N _погл = N - N_omp

придем к формуле

N _погл = (1- σ) N (17.31)

За время τ поверхность приобретает импульс

∆p_S = P_Somp N_omp + Р_Sпогл N _поел

Полученного поверхностью от фотонов, ко времени τ, за которое это приращение произошло:

∆p_S = (1+ σ) N ε cosθ /c. (17.32)

По определению энергия W_nag излучения, падающего на поверхность за время τ, равна произведению интенсивности I излучения на площадь S cos θ поперечного сечения пучка света и на время τ:

W_nag = I S cos θ τ, (17.33)

Используя соотношение (17.27), найдем число фотонов, падающих на по­верхность за время τ:

N= (I /ε )S cosθτ. (17.32)

Подставим это выражение в формулу (17.32). Получим

∆p_S = (1+ σ) (I /c ) cos²θ Sτ

Наконец, формулы (17.21) и (17.22) приводят к следующему выражению для давления, которое оказывает на поверхность плоская световая вол­на, падающая на нее под углом θ:

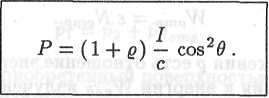
Когда поверхность является зеркальной и отражает все падаюшее на нее излучение (σ = 1), формула (17.34) дает значение

Р_зерк = 2 (I /c ) cos²θ

Если же поверхность является абсолюто черной и поглощает все пада­ющее на нее излучение, то коэффициент отражения σ = 0 и давление излучения на поверхность будет

Р_черн = (I /c ) cos²θ.

Таким образом, давление излучения на зеркальную поверхность оказы­вается в два раза больше, чем на черную.

17.7. Давление изотропного излучения *

Найдем давление, которое оказывает изотропное излучение на плос­кую поверхность. Пусть плотность энергии излучения равна w. Будем рассматривать изотропное излучение как совокупность плоских электро­магнитных волн, распространяющихся по всем возможным направлени­ям в пространстве. Выделим при помощи "узкого" конуса часть волн, направления распространения которых лежат внутри этого конуса (рис. 16.4). Если телесный угол dΩ конуса достаточно мал, то выделенные волны образуют почти плоскую волну, интенсивность dI которой соглас­но формуле (1.20) пропорциональна ее плотности энергии dw:

dI = с dw

Плотность энергии выделенных волн пропорциональна величине телесного угла:

dw=(w/4π)dΩ

Эти соотношения приводят к формуле (16.21)

dI=(сw/4π)dΩ

где согласно (16.24)

dΩ = sin θdθdφ

Давление, которое оказывает на поверхность выделенное излучение, найдем по формуле (17.34), заменив в ней интенсивность I на dI:

dP = (l + σ) (dI /с) cos²θ.

Подстановка выражения (17.37) преобразует эту формулу к виду

dP = (1 + σ)(w/4π) sin θ cos²θ dθdφ.

Для излучения, падающего на какую-либо поверхность из полупростран­ства, угол φ изменяется в пределах от 0 до 2π, а угол θ - от 0 до π/2. Таким образом, давление изотропного излучения будет равно двойному интегралу

P = (1 + σ)(w/4π) 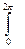dφ 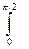sin θ cos²θ dθ

вычисления которого приводят к формуле

P = (1 + σ)(w/6)

Нагретые тела не только отражают и поглощают электромагнитное излучение, но и сами его испускают. Испускаемое телом излучение так­же оказывает давление на его поверхность. Когда наступает равновесие между телом и излучением, от любого участка поверхности тела в полу­пространство уходит излучение, энергия которого равна энергии излуче­ния, падающего из полупространства на этот участок. При этом сумма давлений отражаемого, поглощаемого и испускаемого телом излучений не будет зависеть от свойств поверхности тела. Таким образом, с учетом давления испускаемого телом излучения давление равновесного излуче­ния можно найти по формуле (17.38), положив в ней σ= 1. В результате найдем, что давление равновесного излучения связано с его плотностью энергии соотношением

P =w/3.

_6. АТОМНАЯ ФИЗИКА

Date: 2015-05-19; view: 2541; Нарушение авторских прав