
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Молекула водорода
|
|
Синглетное и триплетное состояния двухэлектронной системы
Рассмотрим теперь двухэлектронную молекулу с одинаковыми ядрами. Принципиальным отличием от одноэлектронной задачи является требование симметрии по отношению к перестановке координат электронов, следующее из принципа тождественности частиц. Электроны являются фермионами, так как имеют полуцелый спин и описываются антисимметричными волновыми функциями по отношению к перестановке пространственных и спиновых переменных. Пренебрегая спин-орбитальным взаимодействием, последние можно считать независимыми и волновую функцию двухэлектронной системы записать в виде произведения
 ,
,
где 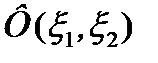 - координатная волновая функция системы,
- координатная волновая функция системы, 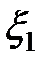 и
и 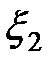 - совокупность пространственных координат первого и второго электронов соответственно,
- совокупность пространственных координат первого и второго электронов соответственно, 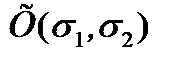 - cпиновая волновая функция,
- cпиновая волновая функция, 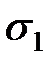 и
и  - спиновые переменные электронов.
- спиновые переменные электронов.
Антисимметричность состояния системы может быть реализована двумя способами:
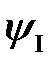
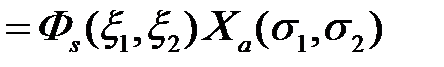
или
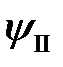
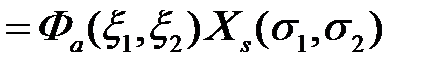 ,
,
где индексы «a» и «s» обозначают соответственно антисимметричные и симметричные состояния. Симметричная спиновая волновая функция, очевидно, соответствует параллельным спинам 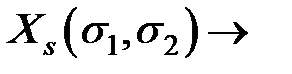 с суммарным спином равным 1 и мультиплетностью, равной трем (мультиплетность - число различных состояний с данным значением спина S, равное 2S+1, отличающихся проекцией спинового момента на выбранное направление z). Такое состояние называется триплетным
с суммарным спином равным 1 и мультиплетностью, равной трем (мультиплетность - число различных состояний с данным значением спина S, равное 2S+1, отличающихся проекцией спинового момента на выбранное направление z). Такое состояние называется триплетным 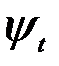 . Антисимметричная спиновая волновая функция соответствует антипараллельным спинам
. Антисимметричная спиновая волновая функция соответствует антипараллельным спинам 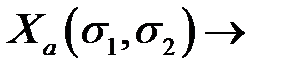 с суммарным спином, равным нулю и мультиплетностью 2S+1=1. Такое состояние называется синглентным.
с суммарным спином, равным нулю и мультиплетностью 2S+1=1. Такое состояние называется синглентным.
Таким образом, двухэлектронная система может находиться в двух состояниях: синглетном 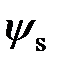 с симметричной координатной волновой функцией и триплетном
с симметричной координатной волновой функцией и триплетном 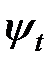 с антисимметричной координатной функцией. Координатным состояниям
с антисимметричной координатной функцией. Координатным состояниям 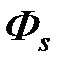 и
и 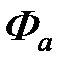 , являющихся решениями уравнения Шрёдингера, соответствуют различные собственные значения энергии системы
, являющихся решениями уравнения Шрёдингера, соответствуют различные собственные значения энергии системы 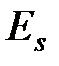 и
и 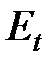 . Поэтому оказывается, что полная энергия двухэлектронной системы зависит от ее полного спина. Взаимодействие электронов, приводящее к такой зависимости называется обменным. Какое из состояний обладает более низкой энергией и реализуется в природе предстоит выяснить непосредственным решением уравнения Шрёдингера для координатной части волновой функции. Впервые такой расчет был выполнен Лондоном и Гейтлером для молекулы водорода
. Поэтому оказывается, что полная энергия двухэлектронной системы зависит от ее полного спина. Взаимодействие электронов, приводящее к такой зависимости называется обменным. Какое из состояний обладает более низкой энергией и реализуется в природе предстоит выяснить непосредственным решением уравнения Шрёдингера для координатной части волновой функции. Впервые такой расчет был выполнен Лондоном и Гейтлером для молекулы водорода 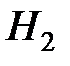 .
.
Задача Лондона - Гейтлера
Рассмотрим процесс образования молекулы 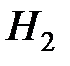 путем бесконечно медленного, адиабатического сближения двух атомов водорода. Потенциальную анергию взаимодействия электронов в поле «чужого» атома будем рассматривать как возмущение, и задачу решать методом теории возмущения. Нулевое приближение соответствует двум изолированным атомам водорода на бесконечном расстоянии друг от друга
путем бесконечно медленного, адиабатического сближения двух атомов водорода. Потенциальную анергию взаимодействия электронов в поле «чужого» атома будем рассматривать как возмущение, и задачу решать методом теории возмущения. Нулевое приближение соответствует двум изолированным атомам водорода на бесконечном расстоянии друг от друга 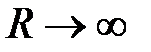 . Пространственные переменные электронов в этом случае независимы и в электронной координатной волновой функции можно разделить переменные
. Пространственные переменные электронов в этом случае независимы и в электронной координатной волновой функции можно разделить переменные
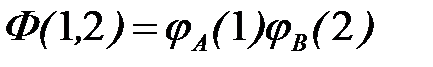 ,
,
где 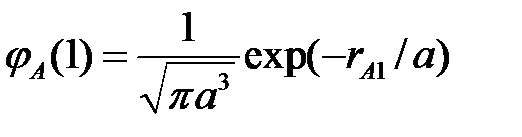 - волновая функция первого электрона в основном состоянии атома водорода на протоне А, а
- волновая функция первого электрона в основном состоянии атома водорода на протоне А, а 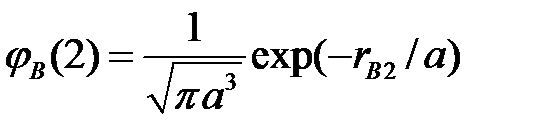 - волновая функция второго электрона в атоме водорода на протоне В. Собственное значение энергии в состоянии Ф (1,2), очевидно, равно удвоенному значению основного уровня атома водорода
- волновая функция второго электрона в атоме водорода на протоне В. Собственное значение энергии в состоянии Ф (1,2), очевидно, равно удвоенному значению основного уровня атома водорода 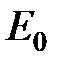 = -27.2 эВ. Поскольку оператор Гамильтона системы тождественных частиц инвариантен по отношению к перестановке координат любой пары частиц, то волновая функция
= -27.2 эВ. Поскольку оператор Гамильтона системы тождественных частиц инвариантен по отношению к перестановке координат любой пары частиц, то волновая функция
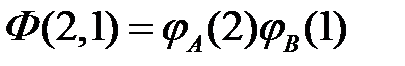 ,
,
где 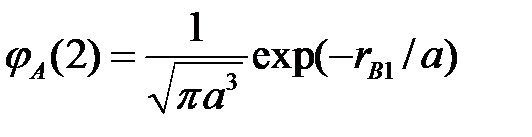 ,
, 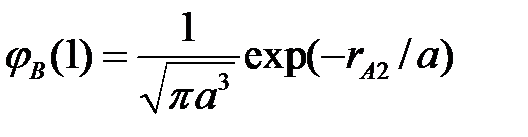 , будет также собственным состоянием с той же энергией
, будет также собственным состоянием с той же энергией 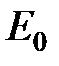 . Таким образом, уровень энергии
. Таким образом, уровень энергии 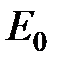 системы в нулевом приближении оказывается двухкратно вырожденным.
системы в нулевом приближении оказывается двухкратно вырожденным.
Поэтому дальнейший ход решения задачи совпадает с таковым для задачи 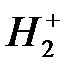 и сводится к решению уравнения Шрёдингера с гамильтонианом
и сводится к решению уравнения Шрёдингера с гамильтонианом 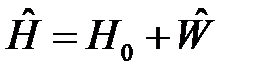 , где
, где 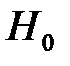 - оператор Гамильтона системы двух невзаимодейству-
- оператор Гамильтона системы двух невзаимодейству-
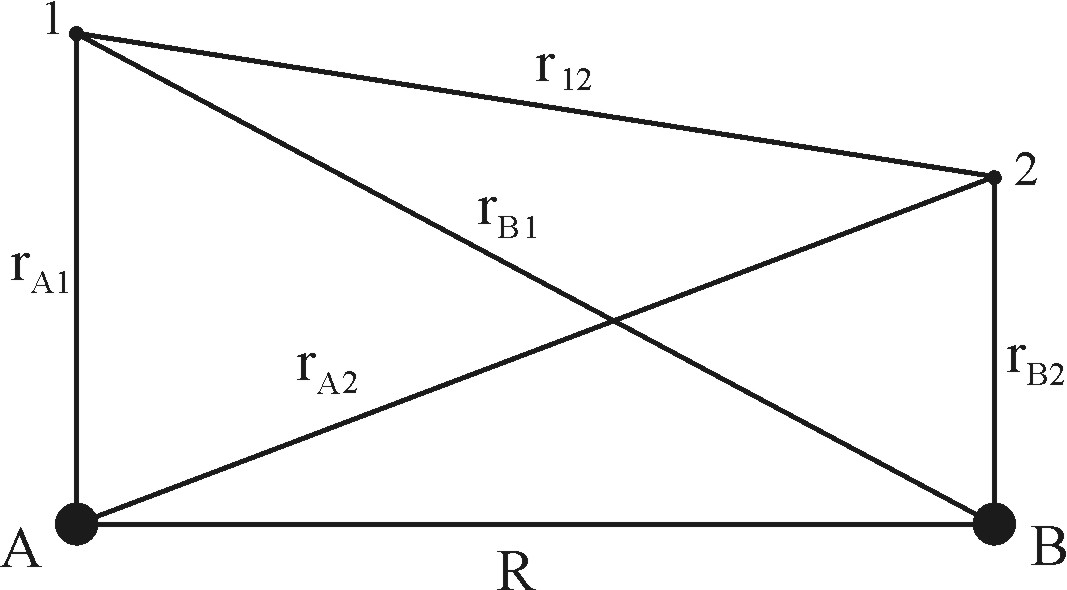
Рис. 4.7. Схема взаимодействий в молекуле водорода
ющих атомов водородa 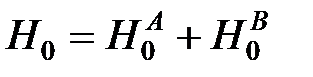 , а
, а 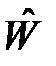 - оператор взаимодействия с «соседями»:
- оператор взаимодействия с «соседями»: 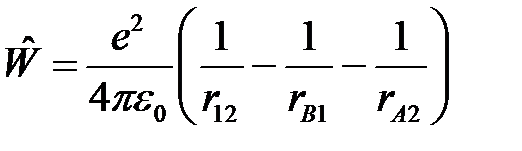 .
.
Согласно теории возмущения в случае двухкратного вырождения с учетом слабого перекрывания (см. задачу  ) для координатных волновых функций молекулы имеем:
) для координатных волновых функций молекулы имеем:
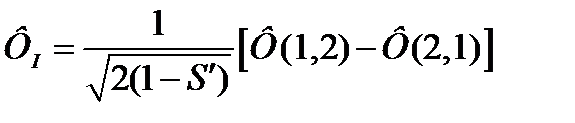 (11)
(11)
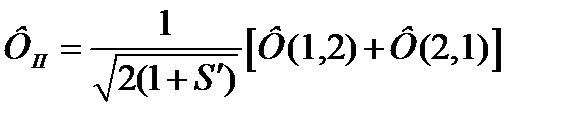
Первая на них является, как видно, антисимметричной и должна умножаться на симметричную спиновую функцию, образуя триплетное состояние молекулы, а вторая, соответственно - на антисимметричную спиновую функцию с образованием синглетного состояния, т. е.
 - триплетное состояние
- триплетное состояние 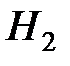 , (12')
, (12')
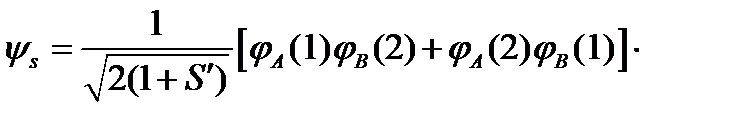 - - синглетное состояние
- - синглетное состояние 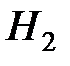 , (12'') которым соответствуют уровни энергии молекулы (см. формулы (8)):
, (12'') которым соответствуют уровни энергии молекулы (см. формулы (8)):
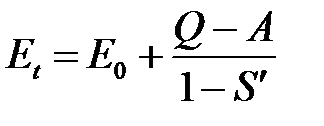 и
и 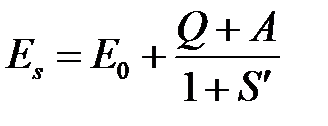 , где
, где 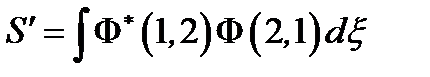 , (13)
, (13)
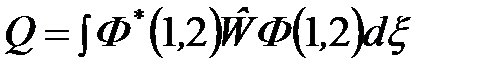 - кулоновский интеграл, (14)
- кулоновский интеграл, (14)
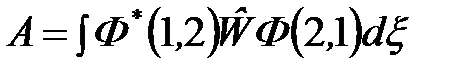 - обменный интеграл. (15)
- обменный интеграл. (15)
Очевидно, 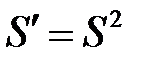 , где
, где 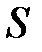 , как и в §4.2.1, интеграл перекрывания атомных орбиталей
, как и в §4.2.1, интеграл перекрывания атомных орбиталей 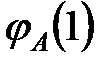 и
и 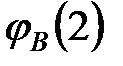
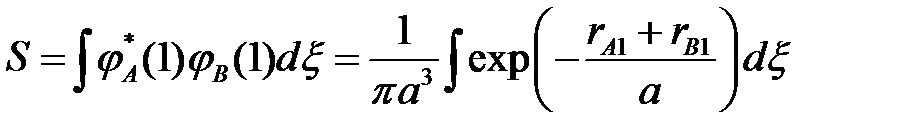 .
.
Кулоновский интеграл 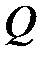 определяет среднюю энергию кулоновского взаимодействия электронов друг с другом и с «чужими» ядрами без учета корреляции, обусловленной симметрией волновых функций
определяет среднюю энергию кулоновского взаимодействия электронов друг с другом и с «чужими» ядрами без учета корреляции, обусловленной симметрией волновых функций 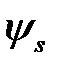 и
и 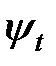 . Интеграл
. Интеграл 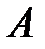 принято называть обменной энергией; она соответствует части электростатического взаимодействия электронов и ядер, связанной с корреляцией в движении электронов, возникающей из-за симметризации волновых функций в соответствии с принципом Паули.
принято называть обменной энергией; она соответствует части электростатического взаимодействия электронов и ядер, связанной с корреляцией в движении электронов, возникающей из-за симметризации волновых функций в соответствии с принципом Паули.
Интегралы 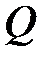 и
и 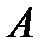 являются функциями расстояния между ядрами
являются функциями расстояния между ядрами 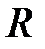 , которое в рамках адиабатического приближения входит как параметр в координатные волновые функции и оператор возмущении
, которое в рамках адиабатического приближения входит как параметр в координатные волновые функции и оператор возмущении 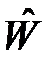 . На рис. 4.8 представлены зависимости от
. На рис. 4.8 представлены зависимости от 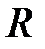 синглетного и триплетного электронных уровней молекулы
синглетного и триплетного электронных уровней молекулы 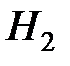 .
.
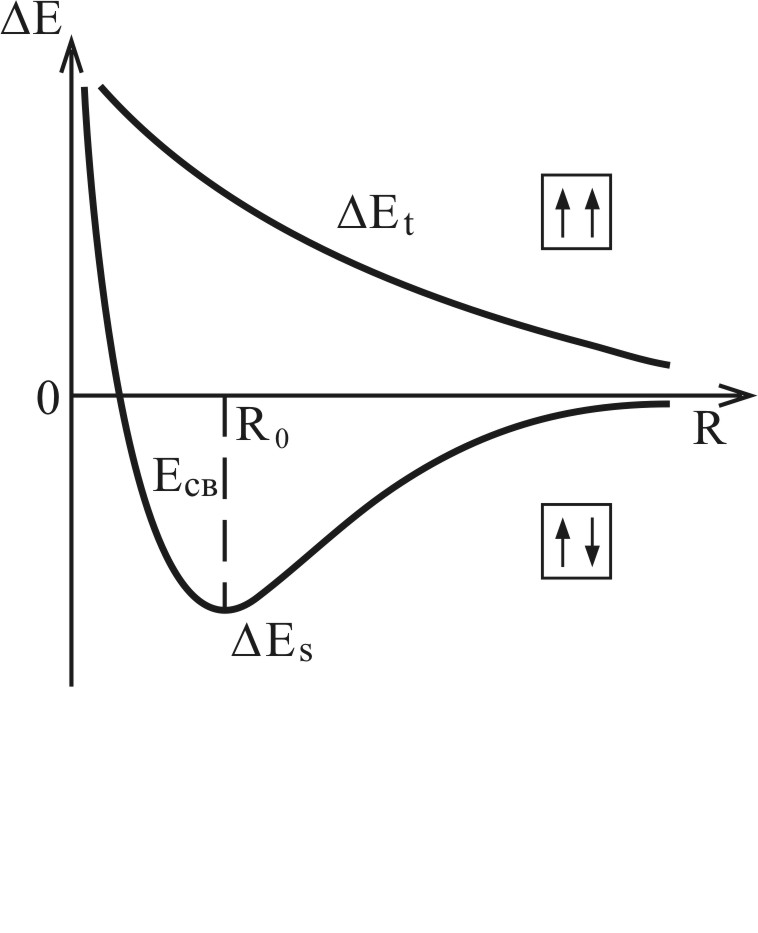
Из рис. 4.9 следует, что при сближении атомов водорода в синглетном спиновом состоянии происходит уменьшение энергии вплоть до расстояния 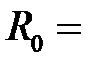 1.4 a = 0.74
1.4 a = 0.74 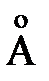 , после чего при дальнейшем уменьшении расстояния наступает резкое увеличение энергии. При сближении атомов в триплетном состоянии энергия монотонно увеличивается, что соответствует отталкиванию атомов.
, после чего при дальнейшем уменьшении расстояния наступает резкое увеличение энергии. При сближении атомов в триплетном состоянии энергия монотонно увеличивается, что соответствует отталкиванию атомов.
Итак, образование молекулы водорода возможно только в синглетном состоянии. Равновесное расстояние между протонами 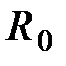 соответствует
соответствует
|
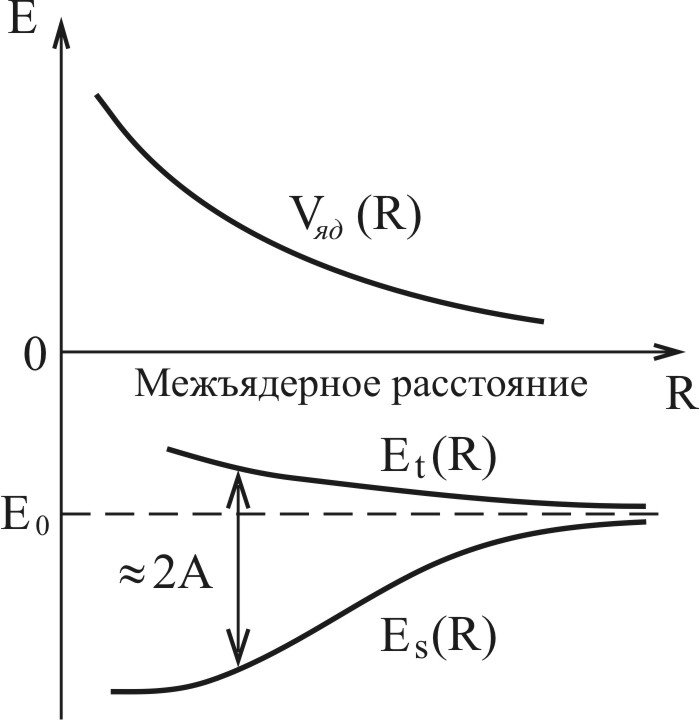
Рис. 4.8. Зависимость от 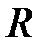 потенциала взаимодействия ядер потенциала взаимодействия ядер 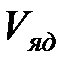 и электронных уровней молекулы H 2 в триплетном ( и электронных уровней молекулы H 2 в триплетном (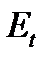 ) и синглетном ( ) и синглетном (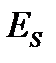 ) состояниях ) состояниях
|
|
Рис. 4.9. Зависимость полной энергии молекулы от межъядерного расстояния R для синглетного и триплетного состояний молекулы  : :
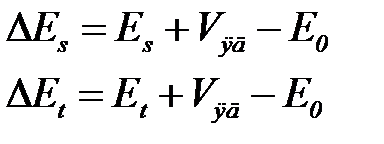
|
минимуму энергии молекулы в этом состоянии, а глубина минимума определяет энергию связи 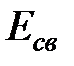 = 4.72 эВ. Разное взаимодействие частиц системы в синглетном и триплетном спиновых состояниях электронов качественно легко понять, анализируя координатные волновые функции (12') и (12''). Функция (12'), соответствующая триплетному состоянию, имеет узел в плоскости, перпендикулярной линии, соединяющей ядра и расположенной посередине между ними, т.к. в этой плоскости
= 4.72 эВ. Разное взаимодействие частиц системы в синглетном и триплетном спиновых состояниях электронов качественно легко понять, анализируя координатные волновые функции (12') и (12''). Функция (12'), соответствующая триплетному состоянию, имеет узел в плоскости, перпендикулярной линии, соединяющей ядра и расположенной посередине между ними, т.к. в этой плоскости 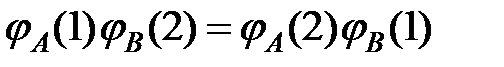 . Функция (12'), соответствующая синглетному состоянию имеет наибольшее значение в этой плоскости. Таким образом, в синглетном состоянии велика вероятность пребывания электронов между ядрами. Электрическое притяжение между электронами и ядрами приводит к связанному состоянию. Разные свойства синглетного и триплетного состояний количественно определяются значением обменного интеграла
. Функция (12'), соответствующая синглетному состоянию имеет наибольшее значение в этой плоскости. Таким образом, в синглетном состоянии велика вероятность пребывания электронов между ядрами. Электрическое притяжение между электронами и ядрами приводит к связанному состоянию. Разные свойства синглетного и триплетного состояний количественно определяются значением обменного интеграла 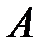 (см. формулы для энергии (13) и рис. 4.8). Из вида этого интеграла (15) видно, что он отличен от нуля лишь в области перекрывания электронных волновых функций обоих атомов и быстро убывают по величине с ростом
(см. формулы для энергии (13) и рис. 4.8). Из вида этого интеграла (15) видно, что он отличен от нуля лишь в области перекрывания электронных волновых функций обоих атомов и быстро убывают по величине с ростом  . Интеграл
. Интеграл 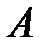 имеет отрицательное значение при
имеет отрицательное значение при 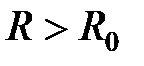 , интеграл
, интеграл 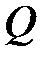 имеет почти везде лишь малое положительное значение, так что
имеет почти везде лишь малое положительное значение, так что 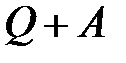 отрицательно при
отрицательно при 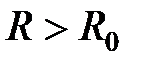 , a
, a 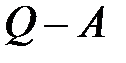 - положительно.
- положительно.
Изложенные выше результаты можно качественно обобщить на двухатомные молекулы с одинаковыми ядрами (гомеополярная связь). Такие молекулы характеризуются, как правило, симметричным распределением электронного облака по отношению к ядрам и отсутствием дипольного момента молекул.
Date: 2015-05-19; view: 1922; Нарушение авторских прав