
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дисперсионные силы
|
|
Дисперсионные силы - силы притяжения, возникающие между атомами или молекулами, у которых в основном состоянии отсутствует дипольный момент (а, зачастую и мультилоли более высоких порядков). Эти силы имеют чисто квантовую природу и не имели объяснения в классической физике. В 1927 г. Уонг рассчитал силы взаимодействия между нейтральными атомами водорода на большом расстоянии, при котором невозможно туннелирование электрона. Его подход был обобщен в начале 30-х годов Лондоном, поэтому соответствующие силы называют силами Лондона или дисперсионными, так как они позволили объяснить дисперсию света в прозрачных средах.
Рассмотрим, для примера, взаимодействие двух атомов благородных газов, дипольный и квадрупольный момент которых равен нулю вследствие высокой сферической симметрии заполненных электронных оболочек. Если, однако, сместить электронную оболочку относительно ядра, то возникнут нескомпенсированные силы притяжения в атоме, возвращающие электронное облако в исходное состояние с высокой симметрией. На этом основании можно говорить об упругости электронных оболочек и рассматривать изолированные атомы как гармонические осцилляторы. Вследствие существования нулевых колебаний любой атом обладает осциллирующим дипольным моментом 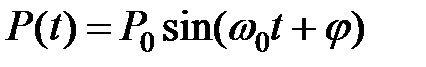 , который создает в пространстве переменное электрическое поле. Таким образом, взаимодействие атомов можно уподобить взаимодействию двух осциллирующих с одинаковой частотой диполей. Как известно из теории колебаний, в системе двух взаимодействующих осцилляторов возникают две новые частоты (нормальные частоты системы) одна из которых выше, а другая ниже исходной
, который создает в пространстве переменное электрическое поле. Таким образом, взаимодействие атомов можно уподобить взаимодействию двух осциллирующих с одинаковой частотой диполей. Как известно из теории колебаний, в системе двух взаимодействующих осцилляторов возникают две новые частоты (нормальные частоты системы) одна из которых выше, а другая ниже исходной 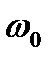 . Система «сваливается» в состояние с меньшей энергией, отвечающей меньшей частоте, что соответствует возникновению сил притяжения между осцилляторами (диполями). Поэтому дисперсионные силы обусловлены понижением энергии нулевых колебаний и имеют универсальный характер.
. Система «сваливается» в состояние с меньшей энергией, отвечающей меньшей частоте, что соответствует возникновению сил притяжения между осцилляторами (диполями). Поэтому дисперсионные силы обусловлены понижением энергии нулевых колебаний и имеют универсальный характер.
Наиболее важной характеристикой типа связи является потенциал парного взаимодействия. Для его описания рассмотрим подробнее задачу взаимодействия двух осциллирующих атомов. Потенциальная энергия взаимодействия двух диполей в определенный момент времени дается выражением (3). Учитывая, что 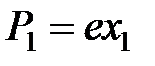 , а
, а 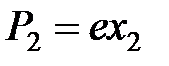 , где
, где 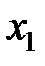 и
и 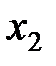 - смещение электронных оболочек атомов, запишем (3) в виде
- смещение электронных оболочек атомов, запишем (3) в виде
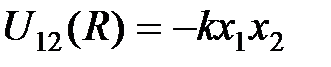 , (7)
, (7)
где 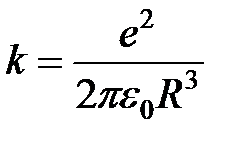 , (8)
, (8)
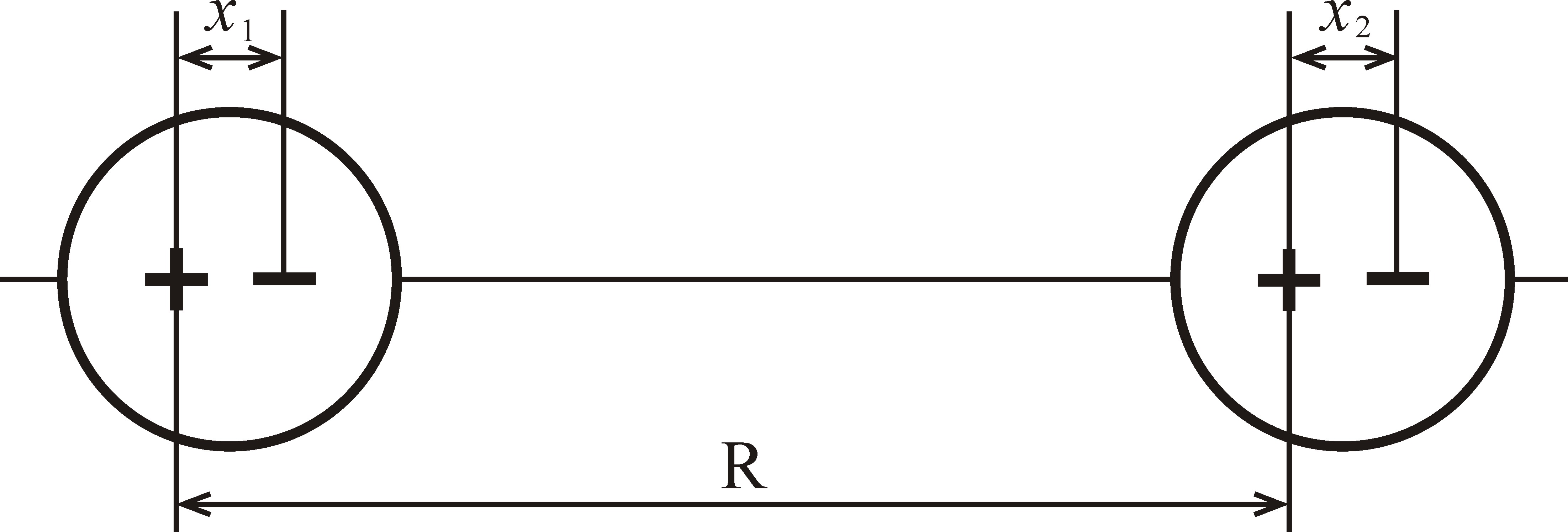
Рис. 4.16. К расчету взаимодействия осциллирующих диполей
Зная энергию взаимодействия диполей, можно найти силы, действующие на осцилляторы. На первый осциллятор со стороны второго действует сила 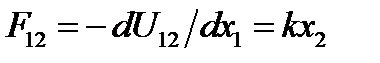 , а на второй со стороны первого действует сила
, а на второй со стороны первого действует сила 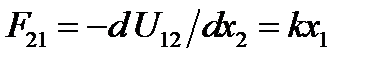 .С учетом этих выражений запишем уравнения движения осцилляторов:
.С учетом этих выражений запишем уравнения движения осцилляторов:
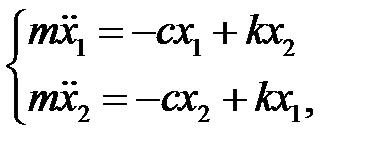 (9)
(9)
где  - коэффициент жесткости электронной оболочки атома, а
- коэффициент жесткости электронной оболочки атома, а 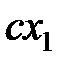 и
и 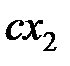 - силы, действующие внутри осциллирующих атомов в отсутствие взаимодействия. Приведем (9) к каноническому виду:
- силы, действующие внутри осциллирующих атомов в отсутствие взаимодействия. Приведем (9) к каноническому виду:
 (10)
(10)
где 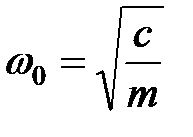 - частота колебаний атомов в отсутствие взаимодействия.
- частота колебаний атомов в отсутствие взаимодействия.
Систему «зацепляющихся» дифференциальных уравнений (10) можно решить методом нормальных координат. Вместо координат 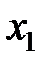 и
и 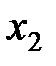 введем новые переменные
введем новые переменные 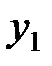 и
и 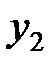 , называемые нормальными координатами, по правилу
, называемые нормальными координатами, по правилу
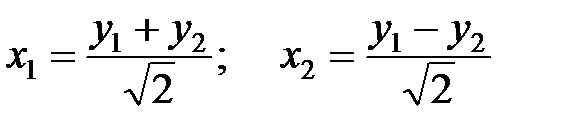 , (11)
, (11)
Подставляя (11) в (10), складывая и вычитая полученные уравнения, обнаружим, что система (10) распадается на два независимых уравнения
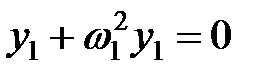 , (12)
, (12)
 , (13)
, (13)
где 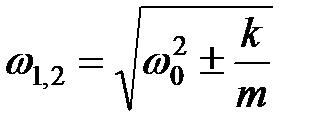 - нормальные частоты системы.
- нормальные частоты системы.
Решая (12) и (13) получим 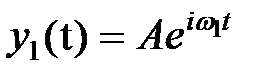 и
и 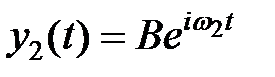 . Нормальные координаты
. Нормальные координаты 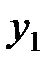 и
и 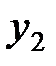 представляют коллективные колебания системы, в которых каждый осциллятор колеблется с одинаковой частотой либо
представляют коллективные колебания системы, в которых каждый осциллятор колеблется с одинаковой частотой либо 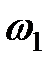 , либо
, либо 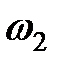 . «Распад» системы уравнений (10) на независимые уравнения (12) и (13) означает, что нормальные колебания не взаимодействуют и полную энергию можно представить в виде суммы энергий отдельных нормальных осцилляторов с частотами
. «Распад» системы уравнений (10) на независимые уравнения (12) и (13) означает, что нормальные колебания не взаимодействуют и полную энергию можно представить в виде суммы энергий отдельных нормальных осцилляторов с частотами 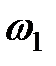 и
и 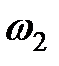 .
.
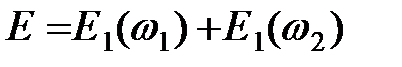 , (14)
, (14)
Такой же результат можно получить, если в выражение для полной энергии системы взаимодействующих одинаковых осцилляторов
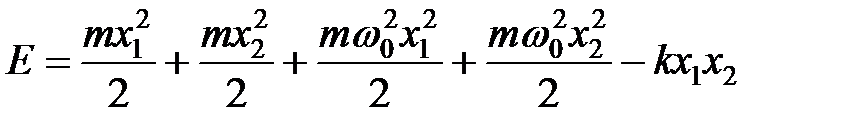
подставить нормальные координаты (11). Тогда в нормальных координатах имеем:
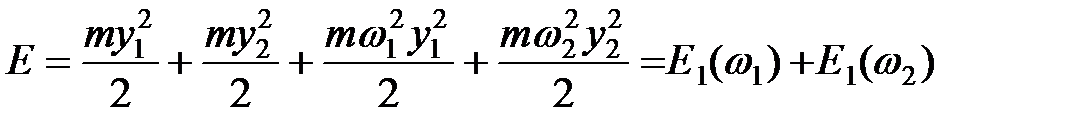 ,
,
что совпадает с (14).
В квантовом пределе энергия системы будет складываться из энергии двух квантовых гармонических осцилляторов с нормальными частотами 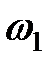 и
и 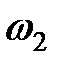 .
.
 , (15)
, (15)
Энергия основного состояния этой системы складывается из энергий нулевых колебаний осцилляторов
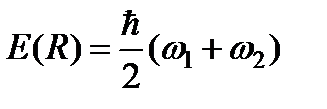 , (16)
, (16)
Энергия Е зависит от относительного расстояния R между диполями (атомами). Для выяснения этой зависимости выразим 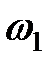 и
и 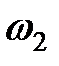 через
через  .
.
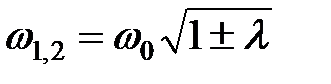 , где
, где 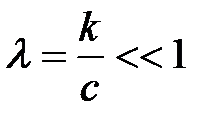 , (17)
, (17)
Разлагая (17) в ряд Тейлора по малому параметру 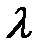
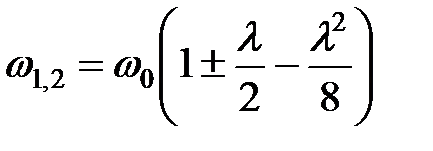
и подставляя в (16), получим
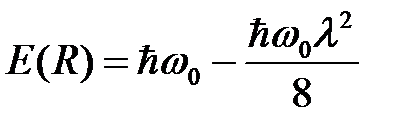 , (18)
, (18)
Энергия двух осцилляторов, разведенных на бесконечность при 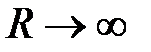 есть сумма
есть сумма 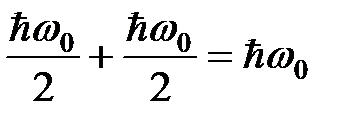 , поэтому разность
, поэтому разность 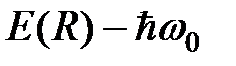 есть работа по удалению осцилляторов на бесконечность, что совпадает с определением потенциальной энергии взаимодействия. Обозначим потенциал парного взаимодействия осцилляторов (атомов) через
есть работа по удалению осцилляторов на бесконечность, что совпадает с определением потенциальной энергии взаимодействия. Обозначим потенциал парного взаимодействия осцилляторов (атомов) через 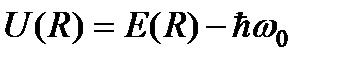 и, учитывая обозначения (8) и (17), окончательно получим
и, учитывая обозначения (8) и (17), окончательно получим
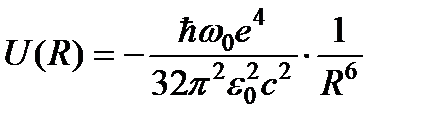 . (19)
. (19)
Это выражение можно привести к более простому виду, если ввести в задачу поляризуемость 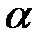 осциллятора. Пусть на осциллирующий с частотой
осциллятора. Пусть на осциллирующий с частотой 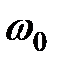 диполь действует постоянное электрическое поле по оси диполя
диполь действует постоянное электрическое поле по оси диполя 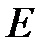 , тогда сила в диполе будет складываться из квазиупругой, равной
, тогда сила в диполе будет складываться из квазиупругой, равной  , и постоянной силы
, и постоянной силы 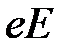 . В равновесии очевидно
. В равновесии очевидно 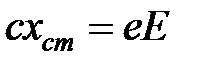 . Величина
. Величина 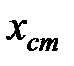 представляет собой смещение центра тяжести осциллирующего заряда (электронного облака) во внешнем поле, поэтому индуцированный дипольный момент
представляет собой смещение центра тяжести осциллирующего заряда (электронного облака) во внешнем поле, поэтому индуцированный дипольный момент 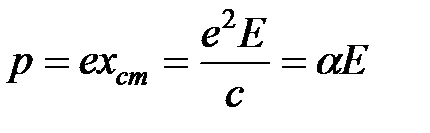 ,т.е.
,т.е. 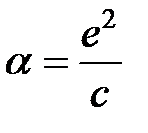 и выражение (19) можно переписать в виде
и выражение (19) можно переписать в виде
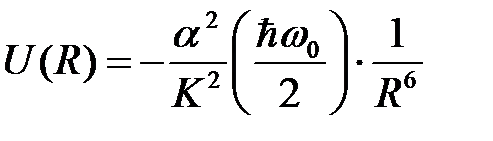 , (20)
, (20)
где 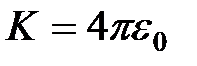 .
.
Энергия притяжения двух одинаковых атомов пропорциональна квадрату поляризуемости атома, нулевой энергии осцилляции электронной оболочки 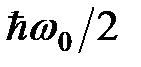 и обратно пропорциональна шестой степени расстояния между атомами. Мы видим, что причиной притяжения является понижение энергии нулевых колебаний системы двух атомов.
и обратно пропорциональна шестой степени расстояния между атомами. Мы видим, что причиной притяжения является понижение энергии нулевых колебаний системы двух атомов.
Таким образом, потенциальная энергия ориентационного, индукционного и дисперсионного взаимодействия убывают с расстоянием как 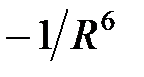 , а соответствующие силы - как
, а соответствующие силы - как 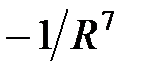 . Потенциал парного взаимодействия сил Ван-дер-Ваальса с учетом сил отталкивания хорошо аппроксимируется потенциалом Леннарда-Джонса
. Потенциал парного взаимодействия сил Ван-дер-Ваальса с учетом сил отталкивания хорошо аппроксимируется потенциалом Леннарда-Джонса
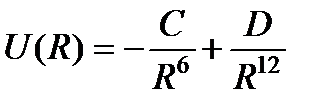 , (21)
, (21)
Силы Ван-дер-Ваальса - самые короткодействующие и слабые из рассмотренных выше сил связи. Их энергия обычно не превышает 0.1 эВ.
Date: 2015-05-19; view: 1449; Нарушение авторских прав