Спиновые функции двухэлектронных состояний

Два электрона с полным спином S и проекцией 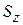описываются спиновой функцией .

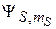Полный спин 1. Пусть спины электронов 1 и 2 направлены вдоль оси z

, .

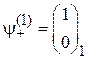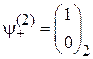Спины складываются как вектора, поэтому двухчастичное состояние имеет спиновые числа 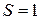, 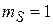и описывается функцией

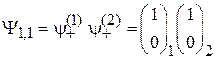. (П.11.14)

Для состояния 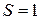, 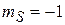аналогично получаем

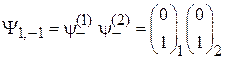. (П.11.15)

Проекция полного спина 0. Состояние

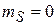
возникает, если проекции спина составляющих частиц имеют противоположные знаки:

,

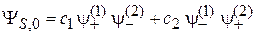где 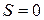, или 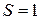. Ищем коэффициенты с ₁ и с ₂.

Для состояния с нулевым полным спином и нулевой проекцией

,

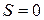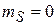
из (7.8) в виде

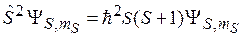
находим

,

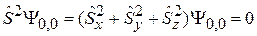тогда

,

,

.

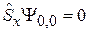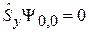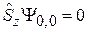Учитывая

,

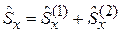получаем:

.

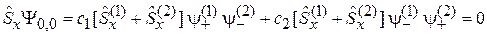Оператор с индексом действует на функцию с тем же индексом. Используя

,

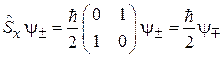находим

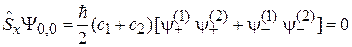
и получаем

.

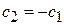Уравнения

,

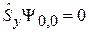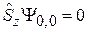
дают тот же результат. Из условия нормировки

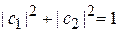
находим

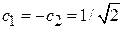
и получаем

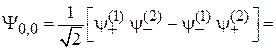
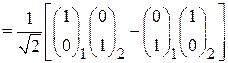. (П.11.16)

Спиновая функция двухчастичного состояния с полным спином 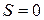антисимметрична при перестановке частиц.

Для единичного полного спина с нулевой проекцией

,

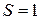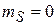
ищем состояние в виде

.

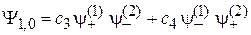Коэффициенты находим из условия ортогональности 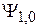состоянию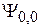

.

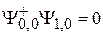Учитывая (7.16)

,

,

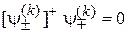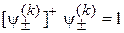и (П.11.16)

,

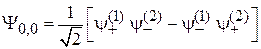получаем

,

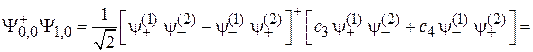
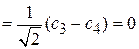тогда

.

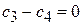С учетом нормировки

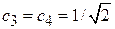
находим

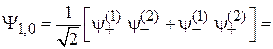
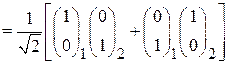. (П.11.17)

Из (П.11.17) и из (П.11.14), (П.11.15)

,

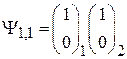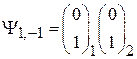
следует, что спиновые функции двухчастичных состояний с полным спином 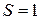симметричны при перестановке частиц.

Перепутанное состояние. Спиновые функции двух частиц (П.11.16) и (П.11.17) имеют вид

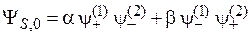. (П.11.18)

Такая форма не представима в виде произведения функций одночастичных состояний и называется перепутанным состоянием двух частиц. Термин ввел Шредингер в 1935 г. В состоянии (П.11.18) частицы 1 и 2 находятся в общем случае в разных местах, имеют неопределенные проекции спина, при этом проекция полного спина равна нулю. Перепутанное состояние двух частиц по спину, по координате или по импульсу получают путем распада на две частицы системы, первоначально находящейся в определенном по этим параметрам состоянии, и не меняющей при распаде эти параметры в силу законов сохранения.

Перепутанные частицы взаимно коррелированны. Пусть полный спин системы равен нулю. Если у частицы 1 измерить проекцию спина на некоторое направление, то возможные результаты 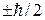. Тогда у частицы 2 состояние изменяется – проекция на то же направление становится 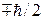. Частицы могут находиться на произвольно большом расстоянии друг от друга и такое преобразование состояния частицы 2 без прямого воздействия на нее означает нелокальность перепутанного состояния. Этот результат получили Альберт Эйнштейн, Борис Подольский и Натан Розен в 1935 г. и рассматривали его как парадокс, опровергающий квантовую механику. Однако, нелокальность перепутанного состояния подтверждена многочисленными экспериментами.

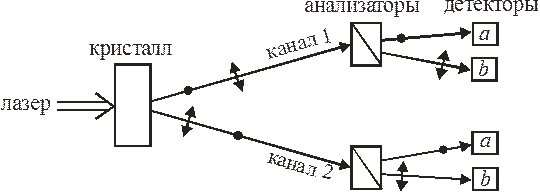
Опыт с перепутанными по поляризации фотонами провел А.В. Белинский в 2002 г. Плоскополяризованное излучение лазера направляется на нелинейный кристалл. На выходе рождаются пары фотонов со взаимно перпендикулярными поляризациями, обозначенными точкой и стрелкой, регистрируемые соответственно детекторами a и b. Один фотон рассеивается в канал 1, другой – в канал 2. Состояние пары перепутано по типам поляризации аналогично. До регистрации частиц не существует определенной поляризации у каждого фотона пары. В одном из каналов с вероятностью 1/2 срабатывает детектор a или b и определяется поляризация соответствующего фотона. В этот момент происходит редукция состояния – становится однозначным результат срабатывания детекторов в другом канале, на каком бы расстоянии эти детекторы ни находились. Каким образом результат регистрации одного фотона мгновенно становится известен второму фотону, если расстояние между ними произвольно велико? Согласно квантовой нелокальности распространяющиеся в пространстве отдельные фотоны отсутствуют до момента их регистрации. В результате измерение создает физическую реальность.

Использовать перепутанное состояние для передачи сообщения с неограниченно большой скоростью не удается. Препятствием является теорема о невозможности клонирования состояния – невозможно унитарным оператором скопировать неизвестное квантовое состояние, не изменив исходного состояния. Поэтому причинность не нарушается.

Кубит. Функция (П.11.18) с условием нормировки 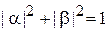образует суперпозицию

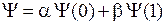
экспериментально различимых состояний

,

,

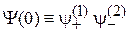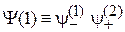и является квантовой единицей информации – кубитом (qubit от англ. quantum bit – «квантовый бит»). Термин ввел Бен Шумахер в 1995 г. В отличие от бита, принимающего значения 0 или 1, кубит Ψ несет значение 0 с вероятностью 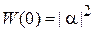и значение 1 с вероятностью 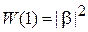. Поэтому кубит содержит информацию в несопоставимо большем объеме, чем бит. Кубиты используются в квантовом компьютере для хранения и преобразования информации.

Date: 2015-05-19; view: 1534; Нарушение авторских прав