Магнитный момент

Аналогия между орбитальным моментом электрона и его спином переносится на соответствующие магнитные моменты.

Орбитальный магнитный момент электрона. Орбитальное движение описывается оператором 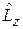с собственным значением

, .

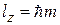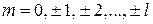Благодаря заряду с орбитальным движением электрона связан магнитный момент с проекцией (1.37)

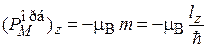, (7.1)

где

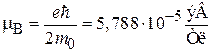– магнетон Бора.

Число проекций магнитного момента равно числу проекций орбитального момента

.

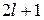Магнитный момент взаимодействует с магнитным полем. Гамильтониан и средняя сила равны

,

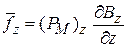. (7.2)

Опыт Штерна–Герлаха. Электрон в основном состоянии атома водорода с 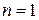, 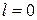имеет 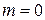и нулевой орбитальный магнитный момент. Влияние протона ядра на магнитные свойства атома пренебрежимо мало, поскольку оно обратно пропорционально массе частицы согласно 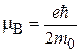. Поэтому магнитное поле не должно действовать на атом в основном состоянии. Этот вывод проверили экспериментально Отто Штерн и Вальтер Герлах в 1922 г. Коллимированный пучок атомов в основном состоянии проходил через расположенное перпендикулярно неоднородное магнитное поле за время t. Оказалось, что исходный пучок расщеплялся на два пучка, отклоняющихся симметрично от начального направления на угол

.

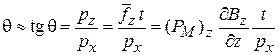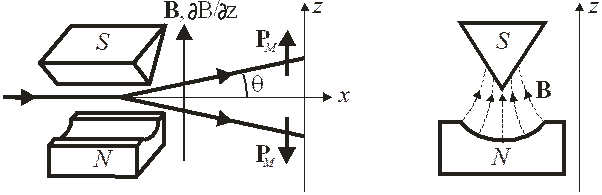
Анализатор Штерна–Герлаха

Противоречие с теорией устранили Джордж Уленбек и Сэмюэл Гаудсмит в 1925 г., введя спин электрона и связанный с ним магнитный момент. По углу θ вычислены проекции магнитного момента электрона

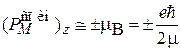. (7.3)

Опыт Штерна–Герлаха дает два спиновых состояния электрона. Исходя из аналогии спина s с орбитальным моментом l, получаем 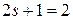, тогда спиновые квантовые числа s, 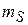и проекция спина 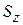равны

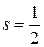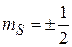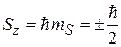, , . (7.4)

Спиновый магнитный момент электрона выражаем через спин. С учетом (7.3) для свободного электрона и для электрона в кристалле

,

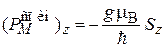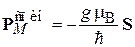, (7.5)

где g – g-фактор (от англ. factor – множитель), другое название «множитель Ландé», ввел Альфред Ландé в 1922 г. Для свободного электрона

.

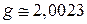В полупроводниках:

; ; ;

; .

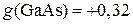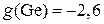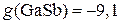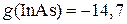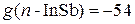Отрицательное значение объясняется переходами между магнитными уровнями валентной зоны и зоны проводимости.

Полный магнитный момент складывается из орбитального (7.1) и спинового (7.5) моментов

. (7.6)

Date: 2015-05-19; view: 554; Нарушение авторских прав