Спин электрона

Собственный угловой момент частицы называется спином от англ. spin – «вращаться». Упрощенное представление – спин – это вращение частицы вокруг своей оси. Физическая природа спина совершенно иная, чем у орбитального момента. Электрон не имеет структуры и является точечным объектом, его собственное вращение не связано с перемещением в пространстве. Теория спина основана на аналогии спина и момента импульса – cоотношения между операторами спина и операторами момента импульса совпадают.

Спин электрона равен 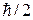. Благодаря заряду и спину электрон имеет магнитный момент, взаимодействующий с электромагнитным полем. Спин проявляется в особенностях спектров атомов, в поведении электронного пучка в магнитном поле, в изменении энергии электрона спин-орбитальным взаимодействием.

В традиционной электронике носителем информации и энергии является состояние заряда. Когерентную суперпозицию таких состояний не удается сохранить длительное время из-за внешних хаотических электрических полей. Спинтроника использует спин для передачи информации, создавая, изменяя и контролируя спин-поляризованный ток. Когерентная суперпозиция спиновых состояний электрона в кремнии существует более 1 с при нормальной температуре, и эта длительность достигает 10 с при 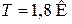, что существенно превышает время в несколько наносекунд, необходимое для преобразования спина. Практическая значимость спинтроники стала очевидной после открытия Альбертом Фертом и Петером Грюнбергом в 1988 г. гигантского магнетосопротивления в многослойной структуре Fe/Cr – ферромагнетик/не ферромагнетик с толщиной слоев меньше длины свободного пробега электрона. При толщине Cr в 12Ǻ намагниченность соседних слоев Fe антипараллельна за счет обменного взаимодействия через электроны проводимости Cr. При наложении магнитного поля напряженностью ~ 20 кЭ намагниченность становится параллельной за время 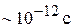. Локальное магнитное поле влияет на спиновый магнитный момент электрона, на его длину свободного пробега (~10 нм), рассеяние и подвижность. В результате изменяется сопротивление между соседними слоями Fe для спин-поляризованного тока. Применение этого эффекта в запоминающих устройствах на жестких дисках увеличило емкость памяти в ~ 600 раз.

Спиновое состояние электрона можно изменять также электрическим полем благодаря спин-орбитальному взаимодействию. Такое поле в полупроводнике создается самой узкозонной гетероструктурой с двухмерным электронным газом, или внешним затвором. По сравнению с магнитным полем электрическое поле можно создать в малом объеме, менять за короткое время, не требуется использовать микромагниты.

Величина спина частицы. В отличие от орбитального момента спин частицы не выражается через координату и импульс. Электрон является точечным объектом, его собственное вращение не связано с перемещением в пространстве. Для спина не применима собственная функция 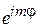оператора 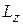, поэтому отсутствует требование целочисленности спина и его проекций, которое следовало из условия периодичности функции

.

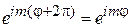Получим допустимые значения квантовых чисел l и m, описывающих модуль и проекцию спина. Используем повышающий и понижающий оператор 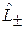, изменяющий число m состояния 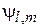с шагом 1. Соотношение (4.18)

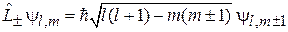
получено из коммутационных соотношений и применимо для спина. Переход между состояниями с минимальной и максимальной проекциями спина

,

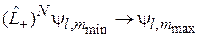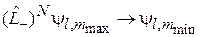
совершается за целое число шагов

.

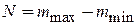Находим 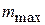и 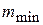из условий отсутствия состояний за пределами интервала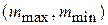

: ,

: .

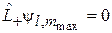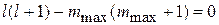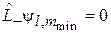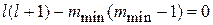Решаем алгебраические уравнения и находим

,

,

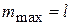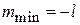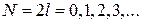
Если N четное, то получаем

, .

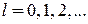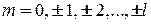Если N нечетное, то

, .

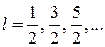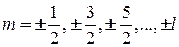Следовательно, возможны частицы с целым спином – бозоны, и частицы с полуцелым спином – фермионы. Названия даны в честь Шатьендраната Бозе и Энрико Ферми. Электрон является фермионом.

Шатьендранат Бозе Энрико Ферми

(1894–1974) (1901–1954)

Date: 2015-05-19; view: 954; Нарушение авторских прав