Вариационный метод. Если возмущение сильное и не выполняется условие применимости теории возмущений

Если возмущение сильное и не выполняется условие применимости теории возмущений

,

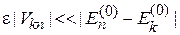то можно приближенно получить состояние системы в аналитической форме по заданному гамильтониану вариационным методом, который разработал Вальтер Ритц в 1908 г. Метод использует функционал энергии в виде среднего от гамильтониана по состоянию системы. Физическое состояние соответствует минимуму функционала. Для получения функционала (функции от функции) задается пробное состояние с набором параметров. Минимум функционала при вариации параметров дает эти параметры, состояние и энергию системы. Метод не позволяет оценить погрешность результата.

Функционал энергии. Стационарная система находится в состоянии y с условием нормировке . Среднее от гамильтониана

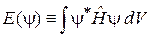(6.48)

рассматриваем как функцию с аргументом 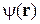. Изучим свойства функционала.

Основное состояние. Собственные функции 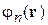гамильтониана с дискретным спектром удовлетворяют

,

.

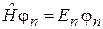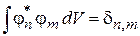Искомое состояние y разлагаем по базису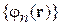

.

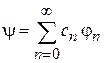Нормировка

требует

.

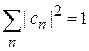Средняя энергия в состоянии y

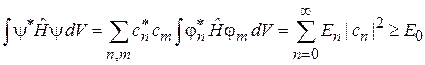
не может быть меньше энергии основного состояния Е ₀, тогда

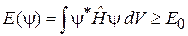. (6.49)

В пространстве нормированных функций y абсолютный минимум функционала энергии равен энергии основного состояния Е ₀. Функция 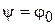, обеспечивающая этот минимум, является волновой функцией основного состояния.

Возбужденное состояние y ортогонально j₀, тогда в разложении

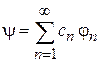
отсутствует слагаемое с j₀. Аналогично предыдущему получаем

.

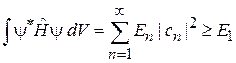В подпространстве нормированных функций y, ортогональных j₀, абсолютный минимум функционала энергии равен энергии первого возбужденного состояния Е ₁. Функция 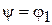, обеспечивающая минимум, является функцией этого состояния.

Аналогично находятся энергии и волновые функции вышерасположенных уровней.

Вариационный метод Ритца для стационарной одномерной системы использует волновую функцию 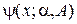с параметрами a и А. Условие нормировки дает 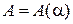. Вариация функции сводится к вариации параметра a. Для функционала энергии (6.48)

условие экстремума

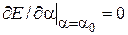(6.50)

дает величину a.

Алгоритм применения метода:

1. Выбираем пробную квадратично интегрируемую функцию основного состояния

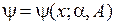
с параметрами α и A, исходя из граничных условий, симметрии, особенностей системы и ее состояния.

2. Нормировка

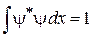
дает .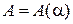

3. Используя гамильтониан системы, вычисляем функционал

.

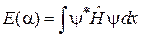4. Условие экстремума

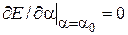
дает a₀ и волновую функцию основного состояния

.

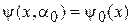Подставляем a₀ в функционал и находим

,

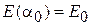ограничивающую сверху энергию основного состояния.

5. Для первого возбужденного состояния выбираем пробную функцию

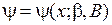
с параметрами β и B, удовлетворяющую условиям ортогональности и нормировки:

,

,

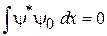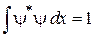и находим .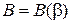

6. Вычисляем функционал энергии с искомой функцией

.

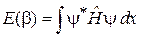Из условия экстремума

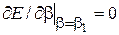(6.51)

получаем b₁, волновую функцию и энергию

,

,

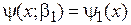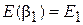ограничивающую сверху энергию первого возбужденного состояния. Аналогично определяются остальные состояния.

Date: 2015-05-19; view: 540; Нарушение авторских прав