Частные случаи возмущений

Постоянное возмущение. При 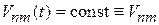из (6.40б) и (6.40в) получаем

,

.

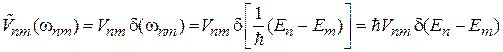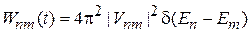Дельта-функция обеспечивает закон сохранения энергии при переходе 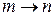. При постоянном возмущении переходы происходят между вырожденными состояниями .

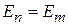Адиабатическое возмущение (от греч. αδιαβάτος – непроходимый) соответствует медленному изменению возмущения. Если матричный элемент 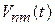изменяется за характерное время 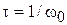, тогда по теореме о частотной полосе фурье-образ матричного элемента 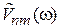мал при 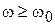. В результате существенны переходы с низкими частотами 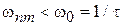, т. е. между близкими уровнями 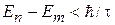. Чем медленнее изменение 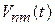, тем ближе уровни, между которыми вероятны переходы.

Периодическое возмущение с частотой w, действующее при :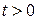

.

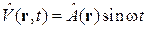Амплитуда перехода (6.39)

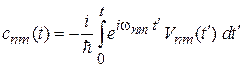
получает вид

,

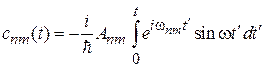где

.

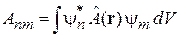Используем формулу Эйлера

.

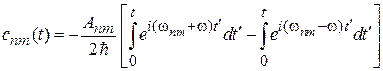Вычисляем

.

Для частоты возмущения w, близкой к частоте перехода 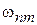, второй интеграл, равный

,

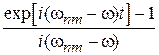гораздо больше первого, тогда

.

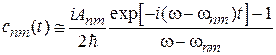Для нахождения вероятности перехода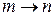

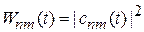
используем

.

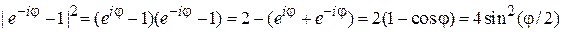Вводим частоту отстройки

,

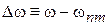получаем вероятность состояния n в момент t

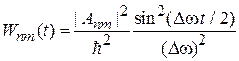. (6.41)

Вероятность перехода 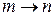за единицу времени

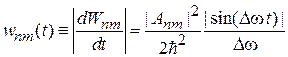. (6.42)

При 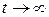с учетом

из (6.42) находим

. (6.43)

Дельта-функция обеспечивает закон сохранения энергии

.

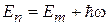Переход 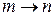совершается, если частота возмущения w равна частоте перехода 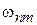и система получает энергию квантом 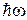, как показано на рис. 1.

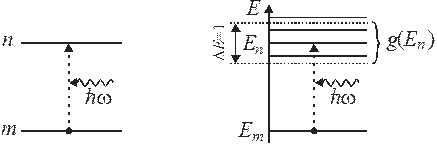
Рис. 1 Рис. 2

Рассмотрим переходы в квазинепрерывном спектре на рис. 2 из состояния m в интервал состояний 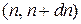. Из (6.43) и из теоремы о сложении вероятностей несовместимых событий, т. е. переходов на соседние уровни, получаем

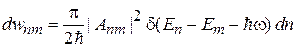. (6.44)

Плотность состояний квазинепрерывного спектра равна числу состояний в единичном интервале энергии, как показано на рис. 2. Плотность состояний около уровня n

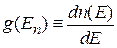. (6.45)

Золотое правило Ферми. Из (6.44) и (6.45) получаем, что под действием периодического возмущения

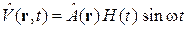
вероятность переходов за единицу времени из начального состояния c энергией 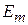в интервал состояний 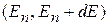равна

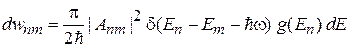. (6.46)

Такой же результат дает возмущение 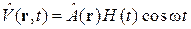. Для возмущения 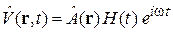вещественная и мнимая части создают одинаковые вклады, и вероятность переходов увеличивается в четыре раза.

Эффект Парселла заключается во влиянии окружения системы на ее спонтанные переходы. Согласно квантовой теории, спонтанные переходы вызваны взаимодействием системы с вакуумными флуктуациями электромагнитного поля, которые зависят от резонатора – полости, где находится система. Фактор Парселла 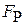равен увеличению вероятности перехода и сокращению времени жизни возбужденного состояния системы при ее помещении в резонатор.

Если собственная частота резонатора близка к частоте перехода, то фактор Парселла достигает максимума и зависит от добротности резонатора, от положения и ориентации излучателя относительно стенок резонатора. Для квантовой точки в микрорезонаторе .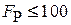

Вне резонанса 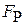уменьшается при уменьшении размера резонатора и плотности состояний в соответствии с (6.46). Если частота излучения ниже наименьшей частоты резонатора, т. е. размер резонатора меньше половины длины волны излучения, то спонтанный переход полностью подавлен.

Эдвард Миллс Парселл в 1946 г. показал, что время жизни возбужденного состояния квантовой системы в резонаторе изменяется из-за изменения плотности конечных состояний.

Квантовый эффект Зенона. Древнегреческий философ Зенон Элейский (ок. 490–430 до н.э.) исследовал возможность движения тела, используя логику, т. е. в рамках строгих рассуждений. Он получил выводы, противоречащие здравому смыслу, названные парадоксами (от греч. παρά-δοξος – странный) – «парадокс Ахиллеса и черепахи» – «быстроногий Ахиллес» никогда не догонит черепаху; «парадокс стрелы» – летящая стрела неподвижна. В них доказывается, что "движения нет", т. е. попытка логически описать движение приводит к его остановке.

Подобное явление обнаруживается у квантового объекта – наблюдение за нестационарной системой, т. е. экспериментальное определение квантового состояния, вызывает возмущение системы и уменьшает скорость переходов и распадов в этой системе. Действительно, вероятность состояния распадающейся системы изменяется с течением времени по нелинейному закону 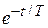, где Т – время перехода. Если состояние измеряется при 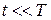, то вероятность исходного состояния велика и процесс измерения «переустанавливает часы на нуль». Непрерывное наблюдение останавливает процесс перехода. Другое объяснение основано на соотношении неопределенностей. Измерение состояния системы уменьшает интервал возможных значений ее энергии 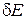, тогда согласно 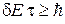увеличивается время пребывания τ в этом состоянии. Явление описали Э. Сударшан и Б. Мисра в 1977 г. Для бозе-конденсата экспериментально обнаружено замедление скорости переходов в 30 раз.

Date: 2015-05-19; view: 602; Нарушение авторских прав