Невозмущенные стационарные состояния

, ,

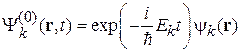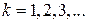удовлетворяют волновому и стационарному уравнениям Шредингера

,

,

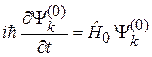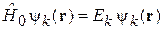и условиям ортонормированности

,

.

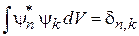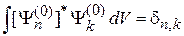Суперпозиция невозмущенных состояний

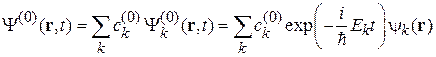(6.30)

имеет неопределенную энергию и удовлетворяет уравнению Шредингера

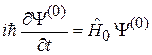. (6.31)

Вероятность обнаружения системы на уровне k с энергией 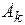равна

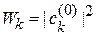, (6.32)

где – амплитуда вероятности обнаружения системы на уровне k.

Возмущенное состояние удовлетворяет уравнению

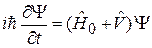, (6.33)

где 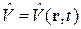. Решение ищем в виде разложения по базису невозмущенных состояний

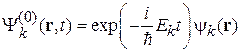
с зависящими от времени коэффициентами

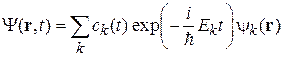. (6.34)

Для нахождения коэффициента 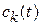подставляем (6.34) в (6.33). Учитываем

,

,

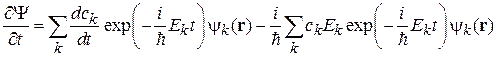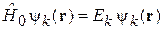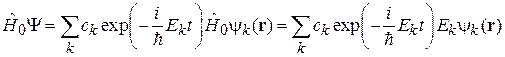
и получаем

.

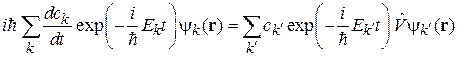Искомые величины 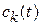, где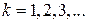

Проектируем уравнение на орт 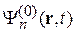. Для этого умножаем уравнение слева на 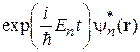, интегрируем по объему и используем

,

.

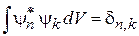Получаем уравнение для коэффициентов

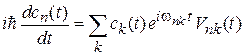, (6.35)

где матричный элемент возмущения

;

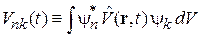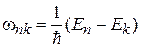(6.36)

– боровская частота перехода с уровня k на уровень n; 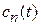– амплитуда вероятности обнаружения системы на уровне n в момент t; вероятность обнаружения системы на уровне n в момент t

.

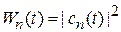Согласно (6.35) быстрота изменения амплитуды вероятности обнаружения системы на уровне n определяется переходами 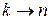со всех уровней k.

Искомый коэффициент разлагаем на два слагаемых

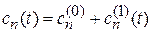, (6.37)

где 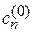– амплитуда вероятности обнаружения системы на уровне n до начала действия возмущения; 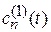– поправка, вызванная возмущением; 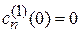поскольку возмущение начинает действовать при 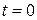. Найдем 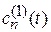, используя теорию возмущений.

Первый порядок теории возмущений. Подставляем (6.37) в (6.35), и ограничиваемся первым порядком возмущения

.

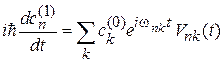Интегрирование по t в пределах 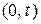с учетом 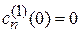дает

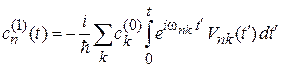. (6.38)

Переход между состояниями. Если при 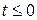система находилась в состоянии m, тогда

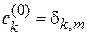
и (6.37) дает

,

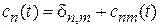где

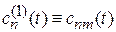
– амплитуда вероятности перехода 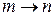в момент t. Правый индекс m соответствует начальному состоянию, левый – конечному. Из (6.38) получаем

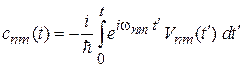. (6.39)

Вероятность перехода 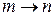, т. е. вероятность обнаружения системы в состоянии n в момент 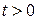, если при 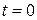было состояние 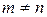, равно

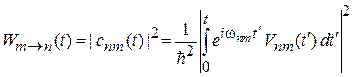. (6.39а)

Для независимого от времени матричного элемента 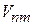из (6.39) и (6.40) находим

,

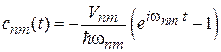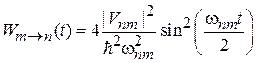. (6.40)

Если в достаточно широком интервале энергии матричный элемент 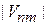и плотность состояний с квазинепрерывным спектром 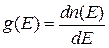остаются постоянными при изменении уровня 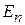, то вероятность переходов с уровня m в интервал получаем интегрированием по энергии. Зависимость от частоты 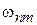в (6.40) быстро убывает при удалении от нуля, поэтому интегрирование выполняем по интервалу 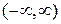изменения энергии. С учетом 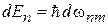вероятность перехода системы с уровня m

.

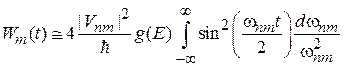Интегрирование дает

.

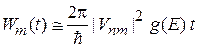Для вероятности переходов за единицу времени получаем золотое правило Ферми

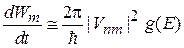. (6.40а)

Число систем в состоянии m. Пусть при 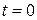имеется 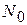независимых систем в состоянии m. Быстрота изменения числа систем в этом состоянии в момент t > 0 пропорциональна вероятности перехода одной системы и числу систем

.

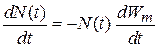Для независящей от времени

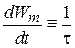
после интегрирования получаем

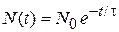. (6.40б)

По истечении времени жизни τ число систем в состоянии m уменьшается в е раз за счет переходов в интервал энергии . Согласно соотношению неопределенностей между энергией и временем

.

Состояние при 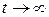. При произвольной зависимости 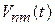по истечении большого промежутка времени интегрирование в (6.39) проводим в бесконечных пределах

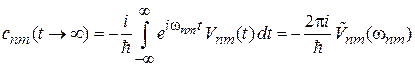, (6.40а)

где фурье-образ возмущения на частоте перехода

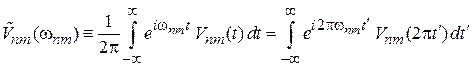. (6.40б)

Амплитуда перехода 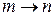при 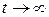пропорциональна фурье-образу возмущенияна частоте перехода. Вероятность перехода

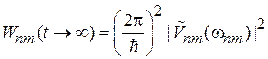. (6.40в)

По истечении большого промежутка времени вероятность перехода системы с уровня энергии m на уровень n пропорциональна квадрату модуля фурье-образа возмущения на частоте перехода.

Date: 2015-05-19; view: 541; Нарушение авторских прав