Стационарных невырожденных состояний

ПРИБЛИЖЕННЫЕ МЕТОДЫ

Точное аналитическое решение уравнения Шредингера удается получить для ограниченного числа одно- и двухчастичных систем. Для других случаев используются приближенные аналитические методы – теория возмущений и вариационный метод, которые позволяют найти уровни энергии и состояния системы.

Возмущением называется малое слагаемое потенциальной энергии системы, дополнительное к исходному гамильтониану, для которого существует аналитическое решение.

Теория возмущений

стационарных невырожденных состояний

Возмущение 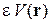входит слагаемым в потенциальную энергию стационарной системы

,

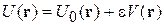где 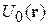– невозмущенная потенциальная энергия; ε << 1 – малый безразмерный параметр. Гамильтониан системы

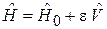
содержит невозмущенную часть

.

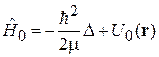Для невозмущенного уравнения Шредингера

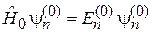(6.1)

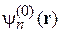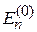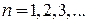с дискретным невырожденным спектром предполагаются известными волновые функции и уровни энергии , где Невозмущенные состояния образуют полный базис 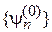с условием ортонормированности

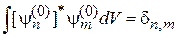. (6.2)

Возмущенные состояния 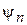удовлетворяют уравнению Шредингера

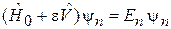. (6.3)

Требуется найти

, .

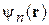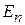Разложение по степеням e. Искомые величины разлагаем в ряды по степеням ε и, пользуясь ε << 1, ограничиваемся первыми тремя слагаемыми

,

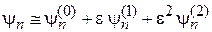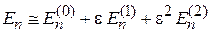. (6.4)

Степень e называется порядком теории возмущений. Подставляем (6.4) в (6.3)

.

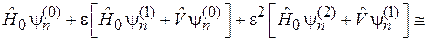
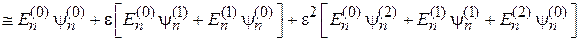Приравниваем коэффициенты при одинаковых степенях ε и получаем для нулевого порядка уравнение (6.1), для первого и второго порядков:

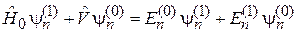, (6.5)

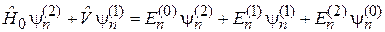. (6.6)

Искомые величины:

, , , .

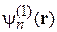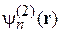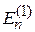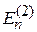Разложение по невозмущенным состояниям. Искомые функции разлагаем по ортонормированному базису невозмущенных состояний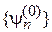

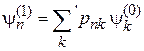, (6.7)

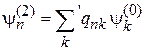, (6.8)

где знак «'» означает отсутствие в сумме слагаемого 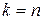, которое учтено в нулевом порядке. Искомые величины:

, , , ,

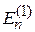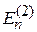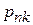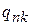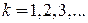
Первый порядок теории возмущений. Подставляем (6.7) в (6.5)

,

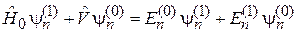учитываем (6.1)

,

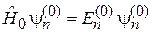получаем

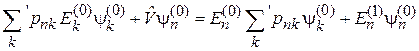. (6.9)

Искомые величины:

, ,

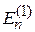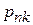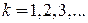
Для получения уравнения с одной неизвестной проектируем (6.9) на орт 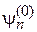. Проектирование в гильбертовом пространстве означает умножение (6.9) слева на 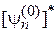, интегрирование по объему и учет ортонормированности базиса

.

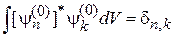В результате получаем

,

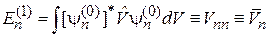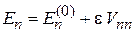. (6.10)

Поправка первого порядка к энергии определяется диагональным матричным элементом оператора возмущения, т. е. равна среднему значению возмущения по невозмущенному состоянию.

Аналогично проектируем (6.9) на орт 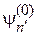, где :

.

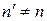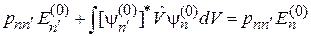Обозначаем 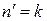и используем матричный элемент оператора возмущения

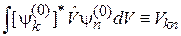, (6.11)

находим коэффициент

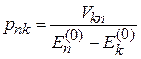. (6.12)

Отсутствие вырождения 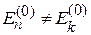обеспечивает конечность 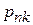. Из (6.4), (6.7) и (6.12)

,

,

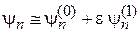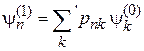в первом порядке теории возмущений получаем волновую функцию возмущенного состояния

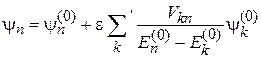. (6.13)

Требование малости поправки к невозмущенной функции 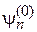дает условие применимости (6.10) и (6.13)

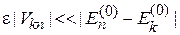. (6.13а)

Свойства первого порядка теории возмущений:

1. Выражение (6.13) не содержит слагаемых с 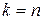, поэтому состояния 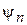нормированные

.

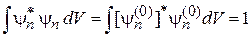2. Диагональный матричный элемент возмущения 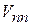дает поправку к энергии 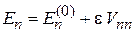и не дает вклада в волновую функцию.

3. Недиагональные матричные элементы 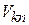не дают вклада в энергию, но определяют поправку к волновой функции.

4. Чем ближе друг к другу уровни невозмущенной системы, тем сильнее изменяется волновая функция.

Второй порядок теории возмущений. Подставляем (6.7) и (6.8)

,

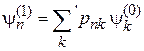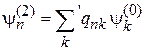
в (6.6)

.

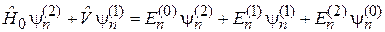Учитываем (6.1)

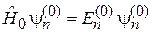
и получаем

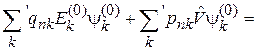
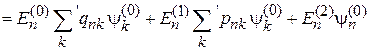. (6.14)

Искомые величины:

, ,

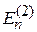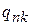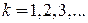
Для получения уравнения с одной неизвестной проектируем уравнение на орт 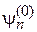, т. е. умножаем (6.14) на 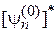, интегрируем по объему и используем ортонормированность базиса

.

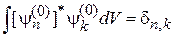С учетом (6.11)

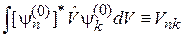
получаем

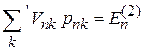
– поправка к энергии во втором порядке. Используя (6.12)

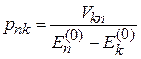
и

,

находим

,

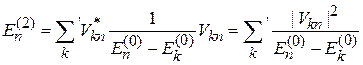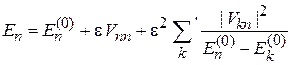(6.15)

– энергия возмущенного состояния до второго порядка, где

.

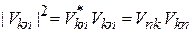Аналогично проектируем уравнение (6.14)

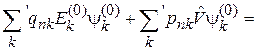
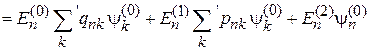
на орт 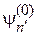, где :

.

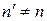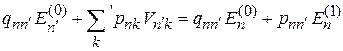Обозначая 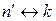и учитывая выражения (6.10) и (6.12) для 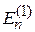и , можно получить

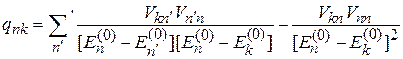. (6.16)

Свойства второго порядка теории возмущений:

1. Из (6.15)

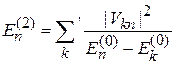
для основного состояния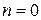

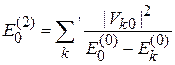
с учетом 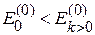получаем 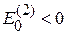. Поправка второго порядка к основному состоянию понижает его энергию.

2. Для двухуровневой системы с учетом 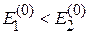из (6.15)

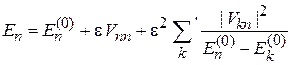
получаем

,

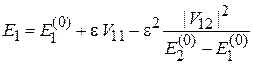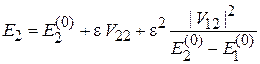. (6.17)

Энергия верхнего уровня увеличивается во втором порядке, энергия нижнего уровня уменьшается. Возмущение во втором порядке раздвигает уровни.

3. Чем ближе уровни энергии, тем сильнее реагирует система на возмущение.

ПРИМЕР

На линейный осциллятор действует ангармоническое возмущение 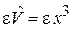. Для основного состояния 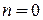найти волновую функцию в первом порядке теории возмущений и энергию в двух порядках.

Из (6.11), (6.13), (6.15) и (3.39) получаем

,

,

, ,

.

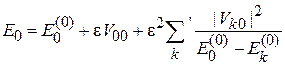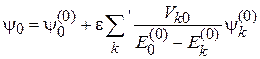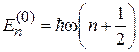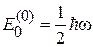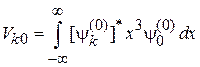Используем (3.34)

,

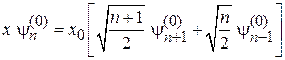где 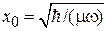, находим

.

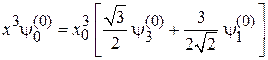Учитываем ортонормированность (3.33)

,

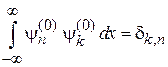получаем матричные элементы

,

.

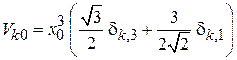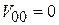В результате

,

.

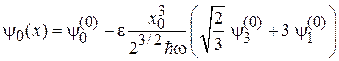Уровень основного состояния понижается.

Date: 2015-05-19; view: 639; Нарушение авторских прав