Возмущение стационарных вырожденных состояний

Для вырожденных состояний 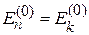рассмотренная теория не применима из-за обращения в нуль знаменателей в (6.13)

,

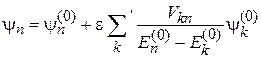в (6.15) и (6.16)

,

.

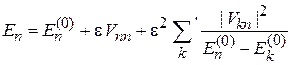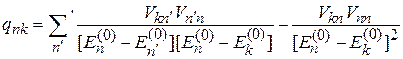Ограничимся далее рассмотрением лишь первого порядка теории возмущений для двукратно вырожденного состояния.

Двукратное вырождение. Невозмущенные вырожденные состояния 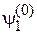и 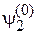ортонормированны

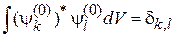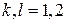, , (6.18)

имеют одинаковую энергию и удовлетворяют стационарному уравнению Шредингера

,

.

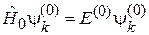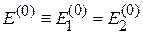Уравнению удовлетворяет также суперпозиция

,

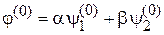где α и β постоянные. Нормировка 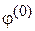обеспечивается условием

.

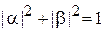Рассматриваем две суперпозиции

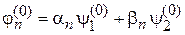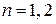, . (6.19)

Возмущение действует на 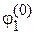иначе, чем на 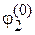. Состояния 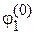и 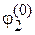получают разные энергии и вырождение снимается. В общем случае система переходит в состояние с неопределенной энергией. Найдем коэффициенты 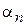и 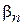из условия, что возмущение в первом порядке не перемешивает 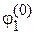и 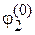, но сдвигает уровни энергии.

Если возмущение обладает определенной симметрией, то она переносится на искомую суперпозицию состояний.

Возмущенные состояния. Повторяем рассуждения предыдущего раздела применительно к состояниям . Используем (6.4) и (6.7)

,

.

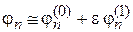Возмущение не перемешивает 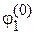и 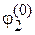, тогда

.

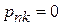Из (6.9)

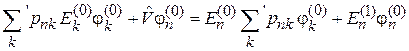
получаем

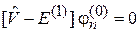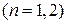, . (6.23)

Подстановка (6.19)

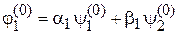
дает

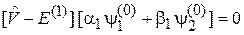. (6.24)

Искомые величины:

, , .

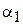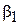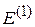Проектируем уравнение на орт 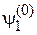, умножая (6.24) слева на 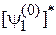и интегрируя по объему. Аналогично проектируем (6.24) на орт 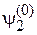. Учитываем ортонормированность (6.18)

,

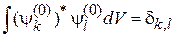получаем однородную систему уравнений

,

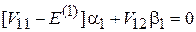, (6.25)

где

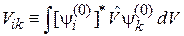
– матричный элемент возмущения между состояниям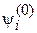и и .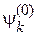

Поправку 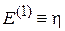к энергии (6.4)

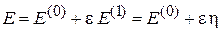
получим из условия разрешимости системы уравнений (6.25)

.

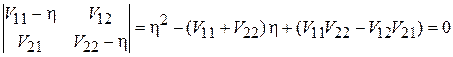Учитываем

,

,

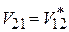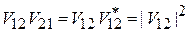находим

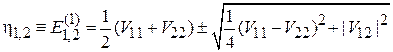(6.26а)

и энергии состояний

,

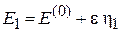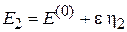. (6.26б)

Энергия соответствует состоянию

,

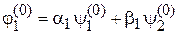энергия 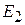соответствует состоянию

.

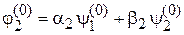Подставляем 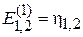в первое уравнение системы (6.25)

,

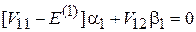находим

,

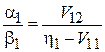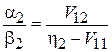. (6.27)

С учетом нормировки

,

,

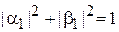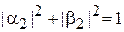получаем две пары уравнений и находим коэффициенты 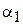, 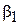и 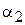, 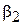для состояний (6.19)

, ,

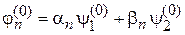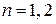которые не перемешиваются возмущением. Эти состояния получают сдвиг энергии (6.26б).

Симметричное возмущение по отношению к 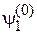и 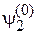означает симметрию матричных элементов 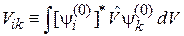в виде

,

.

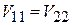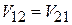Из (6.26а)

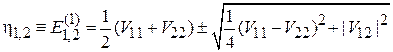
получаем

.

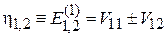Из (6.27)

,

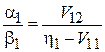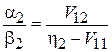
находим

, .

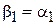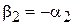С учетом нормировки

,

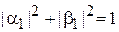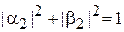
получаем

,

.

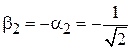Тогда (6.19)

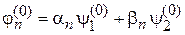
дает возмущенные состояния

,

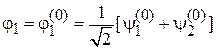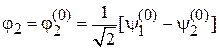. (6.28)

Из (6.26б)

,

,

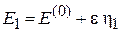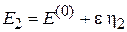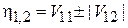
находим

,

,

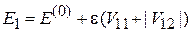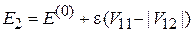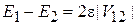. (6.29)

Возмущение отодвигает уровни друг от друга пропорционально энергии возмущения .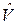

Пример симметричного возмущения. Плоский ротатор является электрическим диполем. Заряды 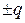расположены на расстоянии L и образуют дипольный момент величиной 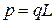. Внешнее однородное электрическое поле E расположено в плоскости ротатора и создает потенциальную энергию

,

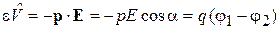где α – угол между полем и дипольным моментом ротатора. Использовано

, .

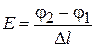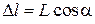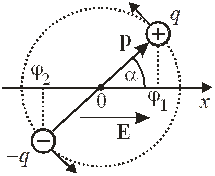
Для плоского ротатора без поля ранее получены уровни энергии и состояния

, ,

.

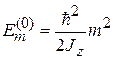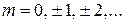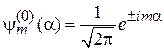При 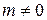вырождены состояния

,

.

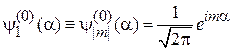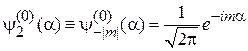Вычисляем матричные элементы

,

,

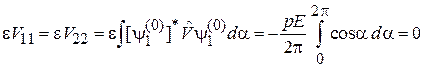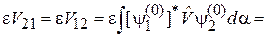
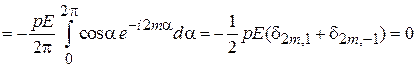где использовано

,

.

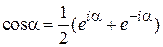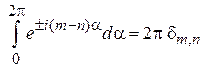Следовательно, возмущение симметричное. Из (6.26)

,

,

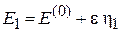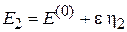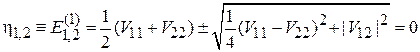
для рассматриваемой системы получаем, что в первом порядке теории возмущений энергии состояний не изменяются.

Суперпозиции состояний, которые не перемешиваются возмущением, находим из (6.28)

,

.

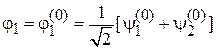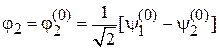Получаем

,

.

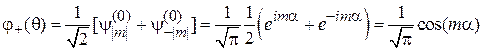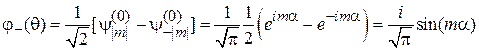Физический смысл результата. Возмущение 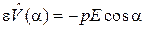четное

,

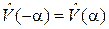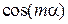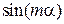поэтому оно сохраняет состояния с определенной четностью: и . Состояния с неопределенной четностью 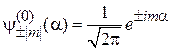перемешиваются.

Date: 2015-05-19; view: 627; Нарушение авторских прав