Эффект Ааронова–Бома. Магнитное и электрическое поля выражаются через потенциалы

Магнитное и электрическое поля выражаются через потенциалы

, .

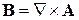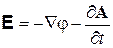В классической электродинамике векторный потенциал , не зависящий от времени, и скалярный потенциал 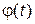, не зависящий от координат, не действуют на заряд. Д. Бом и Я. Ааронов показали в 1959 г., что фаза волновой функции изменяется под действием скалярного и векторного потенциалов, даже в том случае, когда нет силового действия поля на частицу. Эффект Аронова–Бома подтвержден интерференционными экспериментами и свидетельствует о нелокальности квантового состояния.

Магнитный эффект. Пусть заряд q движется перпендикулярно магнитному полю В по замкнутой траектории. Полуклассическое квантование (1.22) 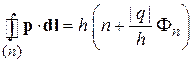, с учетом 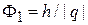дает

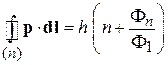, (5.53)

где 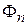– магнитный поток через поверхность, ограниченную траекторией 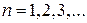Изменение фазы при прохождении частицей траектории n без магнитного поля

.

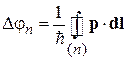Вклад магнитного поля в фазу при движении по замкнутой траектории

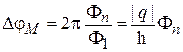. (5.54)

Для незамкнутой траектории между точками r ₀ и r поток обобщается 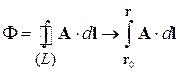, тогда

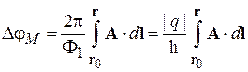. (5.55)

Векторный потенциал изменяет фазу волновой функции.

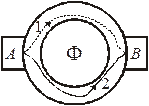
Осцилляции сопротивления проводящего кольца при изменении магнитного потока исследовали Ю.В. и Д.Ю. Шарвины в 1981 г. Кольцо из магния диаметром (1,5¸2) мкм при температуре ~ 1К обеспечивает длину когерентности электронов, превышающую размер кольца. На платиновые контакты А и В подается напряжение. Через кольцо проходит магнитный поток Ф. Электронная волна разделяется на контакте А, идет по путям 1 и 2, набирая фазы φ₁ и φ₂, и интерферирует на контакте В с разностью фаз 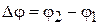. Учитывая, что при обращении движения набираемая фаза меняет знак, из (5.54) получаем

.

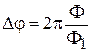Изменение магнитного потока меняет разность фаз. Максимум интерференции 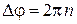, где 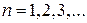, соответствует максимуму тока между контактами. В результате, при изменении магнитного поля сопротивление между контактами осциллирует с периодом

.

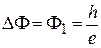Если через кольцо одновременно переносится заряд 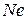, то период осцилляций равен .

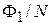Электрический эффект. Фаза волновой функции частицы с постоянной полной энергией 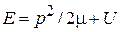изменяется пропорционально времени 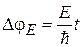. Заряд q, движущийся в течение времени τ в электрическое поле с потенциалом 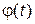, за счет потенциальной энергии 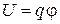набирает дополнительную фазу

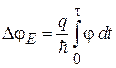. (5.57)

В эксперименте электрон в виде волнового пакета испускается в т. A, проходит через отверстия экрана 1 и 2 и движется внутри проводящих цилиндров, экранирующих электрическое поле 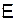. За время движения электрона внутри цилиндров внешнее поле включается, поддерживается постоянным и отключается. На всех этапах движения силовое воздействие на электрон отсутствует. Согласно (5.57) на путях 1 и 2 набирается разность фаз , где 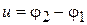– разность потенциалов цилиндров. Максимальный интерференционный ток в цепи соответствует 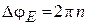, где 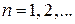, тогда 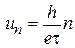. Следовательно, при изменении разности потенциалов ток I и сопротивление цепи осциллируют с периодом

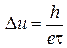. (5.58)

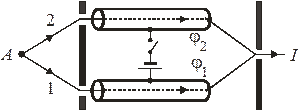
Эффект Зеемана состоит в расщеплении уровней энергии атома в магнитном поле. Явление обнаружил Питер Зееман в 1896 г.

Для электрона в слабом однородном магнитном поле из (5.40) получаем

,

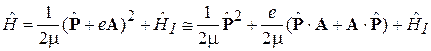где 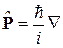; 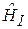– гамильтониан взаимодействия электрона в атоме; отброшено малое слагаемое, пропорциональное 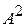. Используем калибровку векторного потенциала

,

, , ,

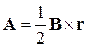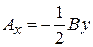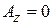тогда

, ,

,

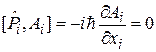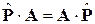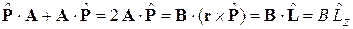где 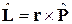– оператор орбитального момента; 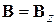. В результате

,

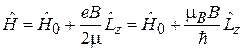где 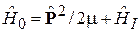– гамильтониан электрона в атоме без учета магнитного поля; 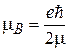– магнетон Бора. Для состояния 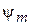с определенной проекцией орбитального момента стационарное уравнение Шредингера

.

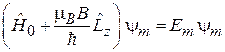Учитывая , находим энергию состояния

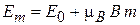, (П.7.16)

где Е ₀ – энергия без учета магнитного поля.

Результат получается и в квазиклассическом приближении. Магнитный момент орбитального движения электрона (1.37) 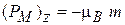, помещенный в магнитное поле , получает дополнительную энергию .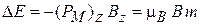

Date: 2015-05-19; view: 884; Нарушение авторских прав