ПРИМЕРЫ. 6.1.Найти состояния плоского ротатора с моментом инерции

6.1. Найти состояния плоского ротатора с моментом инерции .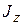

Ротатор – это тело, вращающееся вокруг неподвижной точки, в общем случае закрепленной. Если она совпадает с центром масс и вращение происходит вокруг одной из трех осей инерции, то момент центробежных сил равен нулю, ось вращения неподвижна и тело называется плоским ротатором. Если вращение происходит одновременно вокруг двух или трех осей инерции, то это пространственный ротатор.

При фиксированной оси вращения z используем гамильтониан в цилиндрических координатах (5.15)

.

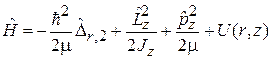При отсутствии радиального движения, движения по оси z и потенциального поля

.

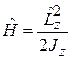Уравнение Шредингера 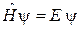получает вид

.

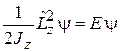Сравниваем с уравнением

,

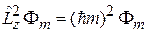которое имеет нормированное решение

.

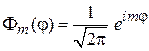Получаем

,

.

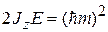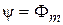В результате 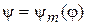– собственная функция оператора ,

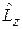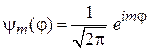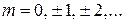, , (П.6.1)

с собственным значением 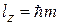. Тогда уровни энергии

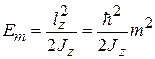. (П.6.2)

Из (П.6.2) находим 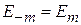, следовательно, уровни вырождены двукратно при .

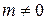6.2. Найти состояния частицы в цилиндрической полости, свободной от полей. Полость радиусом а и длиной образующей s имеет абсолютно непроницаемые стенки.

Система осесимметричная 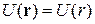, используем цилиндрические координаты, из (5.17) получаем для волновой функции общее решение

.

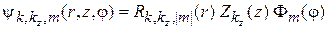Функции

,

, ,

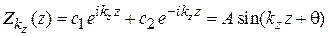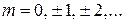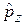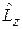являются собственными функциями операторов и . Радиальная функция удовлетворяет уравнению (5.18)

.

При 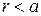учитываем 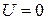, тогда

.

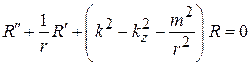Сравниваем с уравнением Ломмеля

,

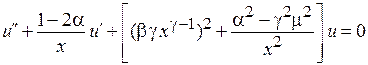имеющим общее решение

,

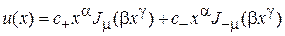где 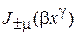– функция Бесселя. Находим параметры

, , , .

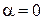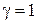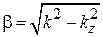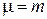Цилиндрическая функция Бесселя при инверсии порядка переходит сама в себя с точностью до постоянной фазы

,

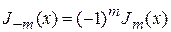тогда общее решение для радиальной функции

.

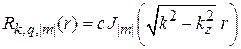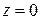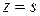Краевые условия на торцах непроницаемой полости при и для

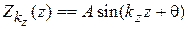
имеют вид

,

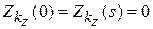откуда находим

, ,

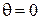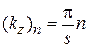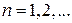
Краевое условие на непроницаемой боковой стенке

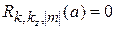
дает

,

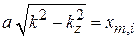где 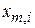– корень функции Бесселя 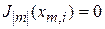; i – порядковый номер корня. В частности

; ; ; ; ; .

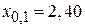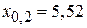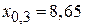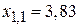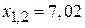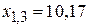В результате получаем возможные значения волнового числа и энергии частицы

,

.

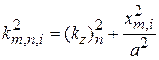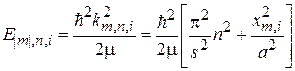Число 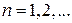характеризует движения по оси z, число 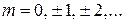– вращение вокруг оси z, число 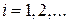– движение в радиальном направлении.

Date: 2015-05-19; view: 1721; Нарушение авторских прав