Магнитное число

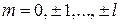
определяет проекцию момента импульса электрона. Число состояний с одинаковым l, т. е. кратность вырождения по l, равна

.

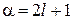Основное состояние имеет , , .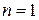

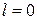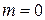Полная энергия. Из (5.21)

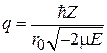
с учетом 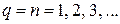получаем квантование энергии

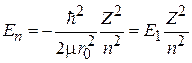, (5.26)

где

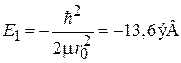
– энергия основного состояния атома водорода. Энергия 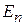не зависит от l и m. Кратность вырождения состояния n равна числу состояний со всеми возможными l и m при одинаковом n. Без учета спина электрона получаем

.

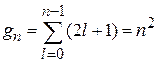Радиальная функция. В (5.25)

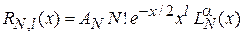
учитываем

, .

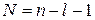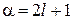Если выбрать

,

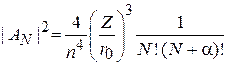то

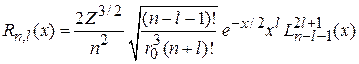(5.27)

и выполняется нормировка

,

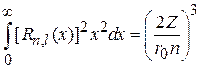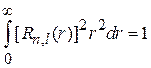. (5.28)

Для атома водорода с 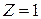находим

, , , ;

,

,

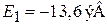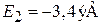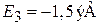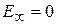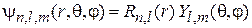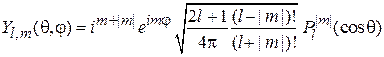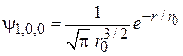– основное состояние,

,

,

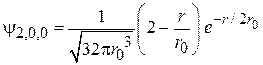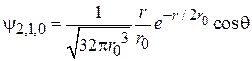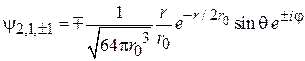. (5.30)

Состояния нормированы

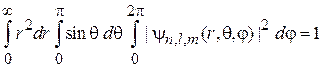. (5.31)

Плотность вероятности по радиальной переменной равна вероятности обнаружения электрона в единичном интервале на расстоянии r от ядра

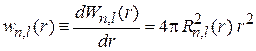, (5.32)

где

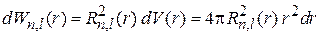
– вероятности обнаружения электрона в шаровом слое радиусом r, толщиной dr; объемом

.

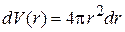Для состояния 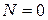находим 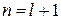. Учитывая 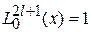, из (5.27)

, ,

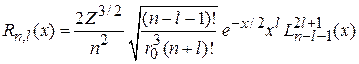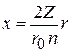для атома водорода 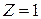получаем состояния с нулевым радиальным числом

.

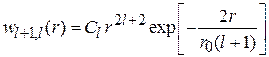Положение максимума плотности вероятности следует из условия

,

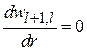находим

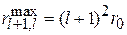. (5.33)

Для 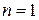, 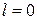получаем 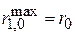– максимум плотности вероятности основного состояния находится на расстоянии r ₀ от ядра, что оправдывает его название – боровский радиус атома водорода.

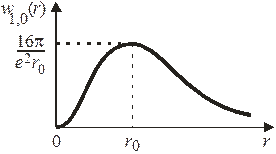
Плотность вероятности состояния 1 s

Орбитали – области наиболее вероятного нахождения электрона в атоме водорода в координатах 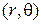, где угол θ отсчитывается от вертикали. Плотность изображения на рисунке пропорциональна

.

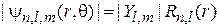Показаны результаты для ; ; .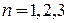

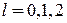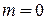l = 0 1 2 n =

Орбитали атома водорода

Ридберговский атом имеет высокоэнергетическое состояние электрона с квантовыми числами 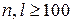. Для возбуждения атома используется лазер с перестраиваемой частотой. Фотоны лазера последовательно переводят электрон с основного на более высокие уровни энергии. Далее электрон локализуют, создавая волновой пакет путем кратковременного облучения атома микроволновым излучением. К такому состоянию применима полуклассическая теория атома Бора. Ридберговский атом достигает макроскопических размеров. Получены возбужденные состояния атома калия с диаметром траектории электрона ~1 мм, что соответствует 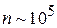. Частоты переходов между соседними состояниями с большими квантовыми числами находятся в микроволновой области, а не в оптической, как для низко возбужденных состояний. Электрический дипольный момент атома 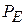пропорционален его размеру, поэтому велика энергия взаимодействия атома с внешним электрическим полем 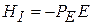и таким атомом легко манипулировать. Время существования ридберговского атома .

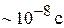Date: 2015-05-19; view: 544; Нарушение авторских прав