Для центрально-симметричной системы

Центральносимметричные и

Осесимметричные СТАЦИОНАРНЫЕ системы

У стационарной системы не зависит от времени потенциальная энергия, тогда гамильтониан

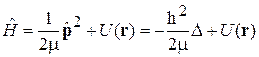. (5.1)

Центральная симметрия означает отсутствие в сферических координатах 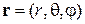угловой зависимости

.

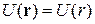Осевая симметрия означает отсутствие в цилиндрических координатах 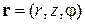угловой зависимости

.

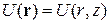Для центрально- и осесимметричных систем сохраняется момент импульса.

Уравнение Шредингера

для центрально-симметричной системы

Если потенциальная энергия системы имеет центр симметрии, т. е. не зависит от углов θ и φ, тогда используется сферическая система координат, в которой .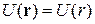

Гамильтониан системы

,

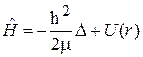где согласно (4.8) и (4.9) оператор Лапласа

,

.

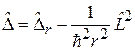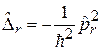В результате

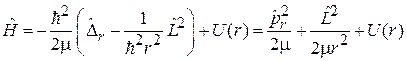. (5.7)

Гамильтониан складывается из кинетической энергии радиального движения, кинетической энергии углового движения и из потенциальной энергии.

Операторы 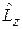и 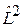коммутируют со всеми слагаемыми гамильтониана

,

,

,

,

.

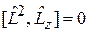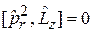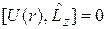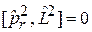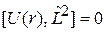В результате

,

.

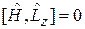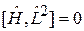Тогда из (2.67)

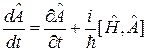
для 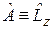и 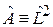получаем

, .

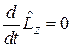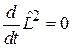Момент импульса и его проекция сохраняются с течением времени и имеют определенные значения вместе с энергией. В результате центрально-симметричное состояние характеризуется собственными значениями операторов 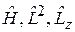, т. е. числами Е, l, m.

Уравнение Шредингера 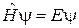с гамильтонианом (5.7) имеет вид

,

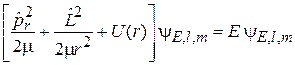где согласно (4.9)

.

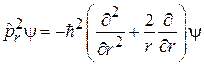Угловое и радиальное движения разделены, решение ищем в виде

.

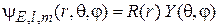Решение подставляем в уравнение, умноженное на 2μ r ² и деленное слева на ψ. Слагаемые с радиальной переменной и с угловыми переменными переносим в разные стороны равенства. Тогда обе стороны не зависят ни от одной переменной

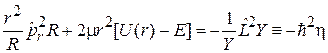, (5.8)

где η – постоянная. В результате получили два независимых уравнения 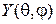– для и для .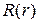

Уравнение

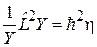
аналогично уравнению (4.14)

,

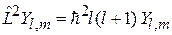следовательно 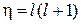, и 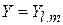– сферическая функция, тогда

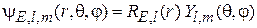. (5.9)

Радиальное уравнение. Для радиальной функции из (5.8) с учетом 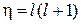получаем

.

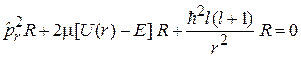Используем

,

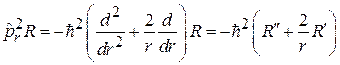находим

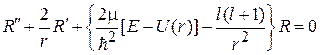. (5.10)

Решение ищем в виде

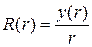. (5.11)

С учетом

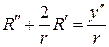
приходим к уравнению

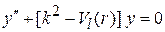, (5.12)

где

;

;

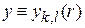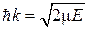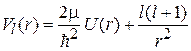. (5.13)

Эффективная потенциальная энергия 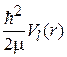складывается из 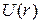и из центробежной энергии отталкивания от оси вращения 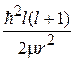.Уравнение (5.12) аналогично одномерному уравнению Шредингера и к нему применимы использованные ранее методы решения.

Конечность 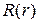при 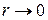требует согласно (5.11) 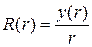выполнения граничного условия

. (5.14)

Ортонормированность для дискретного спектра имеет вид

,

.

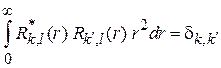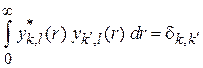Date: 2015-05-19; view: 516; Нарушение авторских прав