Уровни Ландау

Состояния заряда в магнитном поле исследовал Л.Д. Ландау в 1930 г. Получил Нобелевскую премию 1962 г. за работы по сверхтекучести и сверхпроводимости жидкого гелия.

Лев Давидович Ландау (1908–1968)

Рассмотрим состояние заряда q массой μ в однородном стационарном магнитном поле В.

Энергия заряда в полуклассической теории. В плоскости, перпендикулярной магнитному полю, движение происходит по круговой траектории с номером Импульс частицы (1.26а)

.

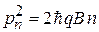Учитываем циклотронную частоту вращения (1.24)

,

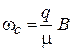находим кинетическую энергию заряда

.

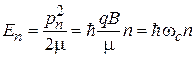Спектр энергии эквидистантный, аналогичный спектру гармонического осциллятора.

Рассмотрим эту задачу в рамках квантовой механики, где отсутствует понятие траектории.

Гамильтониан заряда q в магнитном поле (7.17)

, .

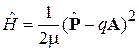В декартовых координатах ось z направляем по полю 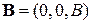. Векторный потенциал связан с индукцией 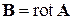, в декартовых координатах

, , .

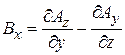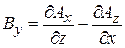Этим соотношениям удовлетворяет потенциал в калибровке Ландау

,

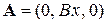тогда

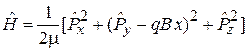. (5.46)

Уравнение Шредингера 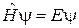получает вид

.

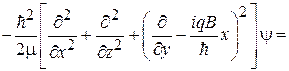
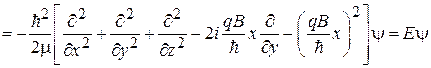Выполняется

, .

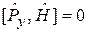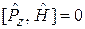Следовательно, состояние характеризуется определенными значениями

, , ,

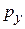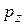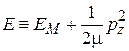а решение содержит произведение собственных функци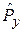й и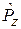

.

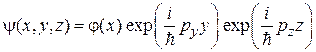Если движение по оси z не ограниченное, то 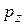– любое вещественное число. Подстановка решения в уравнение и деление его слева на ψ дает уравнение для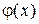

.

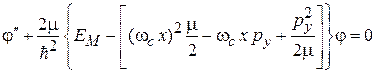Вводим эффективную потенциальную энергию

,

где

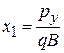, (5.47)

получаем

.

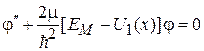Сравниваем с уравнением гармонического осциллятора (3.23)

, ,

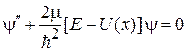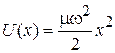имеющего частоту ω и амплитуду нулевых колебаний 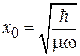относительно точки 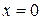. Решаемая задача соответствует осциллятору, колеблющемуся относительно точки 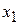с циклотронной частотой 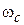и с амплитудой нулевых колебаний

,

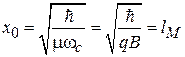равных магнитной длине. Из формулы (3.32) для гармонического осциллятора получаем функцию состояния n

,

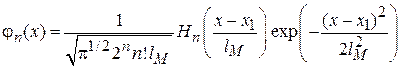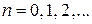
Уровни Ландау. Спектр энергии движения в плоскости 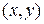совпадает со спектром гармонического осциллятора. Из (3.39) находим

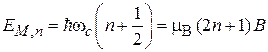. (5.48)

Результат совпал с энергией полуклассической теории с точностью до слагаемого .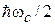

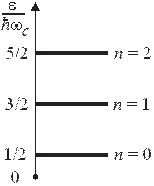
Число состояний на уровне Ландау. Функция состояния 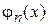зависит от положения центра циклотронного движения 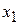, энергия (5.48) не зависит от 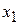, поэтому уровень Ландау вырожден – разным центрам соответствует одинаковая энергия. Найдем кратность вырождения.

Для движения в прямоугольной области со сторонам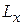и и 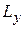условие на положение центра 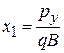по оси x в пределах

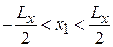
ограничивает импульс

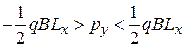
интервалом шириной

.

Ограничение положения частицы по оси y в пределах

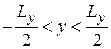
вызывает квантование 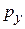. Граничное условие Борна–Кармана (3.8)

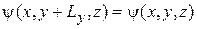
на волновую функцию

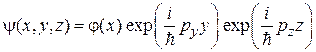
требует

.

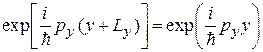Учитывая

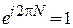, N – целое число,

находим

.

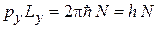Импульс квантуется

,

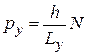соседние значения отличаются на шаг

.

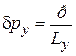Кратность вырождения уровня n

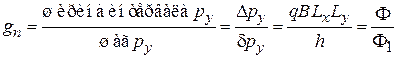, (5.52)

где 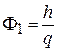– квант магнитного потока. Число состояний на любом уровне Ландаубез учета спина равно числу квантов магнитного потока, приходящихся на область, доступную для движения заряда. В полуклассической квантовой механике число квантов магнитного потока равнялось номеру траектории заряда.

Date: 2015-05-19; view: 1199; Нарушение авторских прав