Граничные условия со скачком потенциала

Квантовые эффекты проявляются, если потенциальная энергия 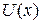существенно изменяется на расстояниях порядка длины волны де Бройля. Этому условию удовлетворяет скачкообразное изменение потенциала, возникающее на границах металла и полупроводника, на примесях и дислокациях, в полупроводниковых гетероструктурах. Различают скачки 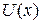: конечный, δ-образный и бесконечный. Конечный скачок существует, например, на границе металла или полупроводника с вакуумом. δ-образный скачок описывает точечное возмущение, например, атом в кристалле. Бесконечный скачок является упрощающим приближением, когда энергия частицы гораздо меньше величины конечного скачка.

Конечный скачок δ-образный скачок Бесконечный скачок

Условия «сшивания» на границе участков получаем однократным и двукратным интегрированием уравнения Шредингера по бесконечно малому интервалу координат около точки скачка потенциала.

Конечный скачок потенциала при 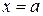. Выполняем двукратное интегрирование уравнения (3.1)

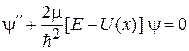
по интервалу 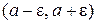, где . Для конечной функции 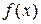используем

,

.

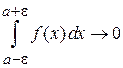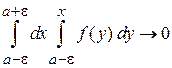Второе и третье слагаемые уравнения дают нули, для первого получаем

,

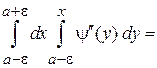
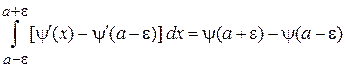где 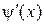считается конечной. В результате

,

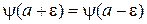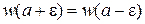. (3.11)

Волновая функция и плотность вероятности непрерывны в точке конечного скачка потенциала.

Однократное интегрирование

,

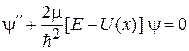вычисляется аналогично и дает

.

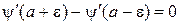Первая производная волновой функции и плотность тока вероятности непрерывны в точке конечного скачка потенциала

,

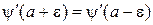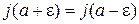, (3.12)

где использована проекция плотности тока вероятности (2.72)

.

Date: 2015-05-19; view: 712; Нарушение авторских прав