Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Частные случаи одномерных стационарных состояний
|
|
Свободная частица. При отсутствии внешнего поля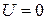 
, уравнение (3.2)
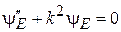
с волновым числом
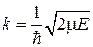
имеет общее решение
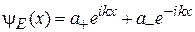. (3.3)
Составляющие бегущие волны
распространяются по- и против оси x с комплексными амплитудами 
. Если краевые условия не накладываются, то спектр непрерывный 
.
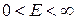Движение частицы создает плотность тока вероятности. Подставляем (3.3) в (2.72)
,
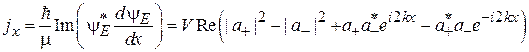где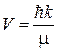 
– скорость частицы. В круглой скобке сумма двух последних слагаемых чисто мнимая, в результате проекция плотности тока вероятности на ось x
,
,
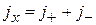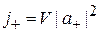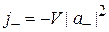. (3.6)
Для частицы с зарядом е и энергией Е задаем плотности электрического тока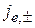 
, получаем плотности тока вероятности 
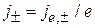, и находим модули амплитуд волн 
.
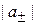Частица в потенциальном ящике. Для частицы ящик размером L является потенциальной ямой. Внутри ящика потенциальная энергия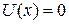 
и частица с энергией Е описывается уравнением (3.2)
,
где
.
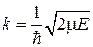Уравнению удовлетворяет решение в виде бегущих волн
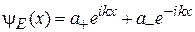(3.7а)
с комплексными амплитудами , или стоячих волн
(3.7б)
с вещественными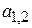 
. Стоячие волны возникают при сложении бегущих волн 
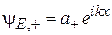и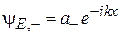 
. Решение (3.7б) не содержит мнимых слагаемых и удобно для записи граничных условий.
Стенки ящика в виде потенциального барьера ограничивают возможные значения волнового числа k. Не используя конкретную форму потенциальной энергии стенок, рассмотрим систему повторяющихся ящиков. Стенки удовлетворяют периодическому условиюБорна–Кармана
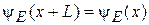. (3.8)
При подстановке (3.7а) условие выполняется, если
.
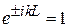Учитывая
, 
,
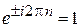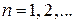находим
.
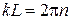Следовательно, волновое число и импульс частицы квантуются
,
.
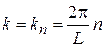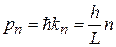Допустимы дискретные уровни энергии
,
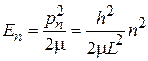где 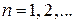– главное квантовое число. Длина волны де Бройля на уровне n
,
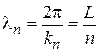тогда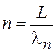 
показывает число длин волн, укладывающихся на ширине ящика, или число полуволн, приходящихся на длину траектории. Расстояние между уровнями
.
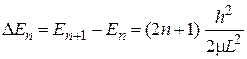Для кристалла с характерным размером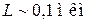 
получаем 
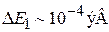. Сравниваем с тепловой энергией частицы газа при нормальной температуре
.
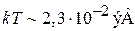При высокой температуре и большом ящике тепловая энергия превышает расстояние между уровнями, дискретность спектра не проявляется и спектр энергии квазинепрерывный.
При низкой температуре и малом ящике тепловой энергии не хватает для перевода системы между уровнями и существенна дискретность спектра.
Состояние n занимает в координатном пространстве объем, равный размеру ящика:
,
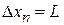в импульсном пространстве неопределенность
,
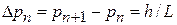в фазовом пространстве
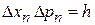. (3.9)
Любое состояние n в одномерном потенциальном ящике занимает фазовый объем, равный постоянной Планка – основное положение статистической теории, следующее из соотношения неопределенностей.
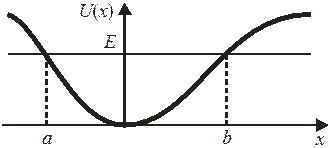
Частица в области, недоступной для классического движения. У стенки ящика при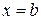 
полная энергия частицы равна потенциальной энергией 
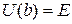, кинетическая энергия и импульс обращаются в нуль, частица останавливается. При 
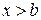вне ящика:
,
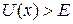кинетическая энергия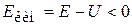 
, импульс 
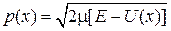– мнимый, поэтому классическая частица не существует.
Уравнение Шредингера
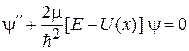
при 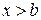получает вид
,
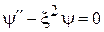где коэффициент затухания
; .
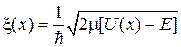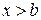Уравнение имеет не равное нулю решение. Квантовая частица обнаруживается вне потенциальной ямы с некоторой вероятностью благодаря туннельному эффекту. При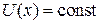 
, 
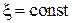общее решение
, .
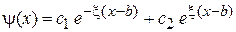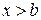Нормировка
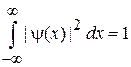
в области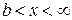 
выполняется только для убывающего с ростом x частного решения. Полагаем 
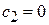, получаем
.
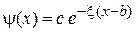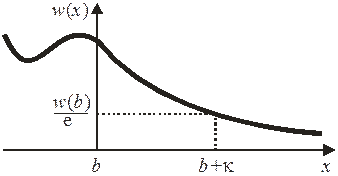
Плотность вероятности обнаружения частицы экспоненциально уменьшается при удалении от края ямы
,
где расстояние затухания
.
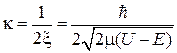В частности
, 
,
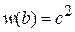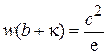κ – расстояние от края ямы до места, где вероятность обнаружения частицы уменьшается в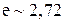 
раз. Чем больше 
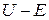, тем меньше κ и быстрее уменьшается вероятность с удалением от края ямы.
Date: 2015-05-19; view: 468; Нарушение авторских прав