Линейный гармонический осциллятор

Гармонический осциллятор колеблется по гармоническому закону. В области применимости квантовой механики он имеет эквидистантный спектр энергии с не равной нулю минимальной энергией. Поэтому состоянию n сопоставляют n квантов энергии. Электромагнитное поле в резонаторе и в свободном пространстве, упругие колебания узлов кристалла, колебания атомов в молекуле рассматриваются как гармонические осцилляторы.

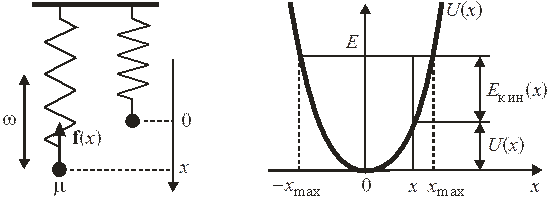
Осциллятор в классической теории. При смещении x от положения равновесия тела массой μ потенциальная энергия и возвращающая упругая сила с коэффициентом жесткости κ равны

,

.

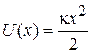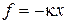Из второго закона Ньютона

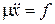
получаем уравнение

,

где

,

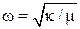и решение

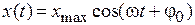
в виде колебания с амплитудой 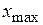и частотой 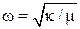. Тогда

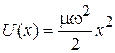. (3.23)

При максимальном отклонении

,

.

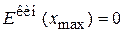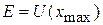Подставляем (3.23) и находим амплитуду колебаний

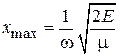. (3.24)

Осциллятор в квантовой теории. В уравнении Шредингера с потенциальной энергией (3.23)

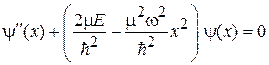(3.26)

переходим к безразмерному аргументу

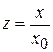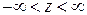, , , (3.27)

.

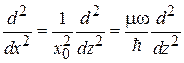Уравнение получает вид

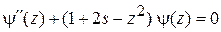, (3.29)

где

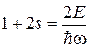. (3.30)

Согласно курсу «Методы мат. физики» при целочисленном 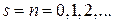решение выражается через полином Эрмита

.

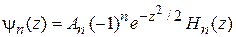При s не целом 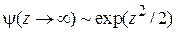, условие нормировки 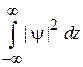не существует, физическое решение отсутствует.

Из теории полиномов Эрмита получаем условие ортонормированности

.

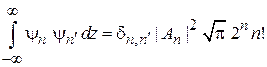Выбор

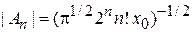
дает

,

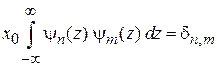тогда

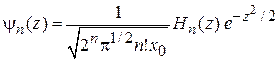. (3.32)

Учитывая 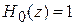, , , 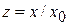из (3.32) находим

,

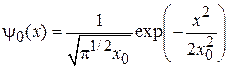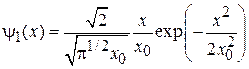. (3.32а)

Ортонормированность и рекуррентные соотношения. Из результатов прошлого семестра:

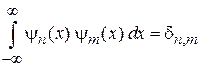, (3.33)

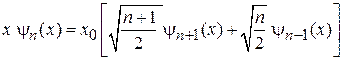, (3.34)

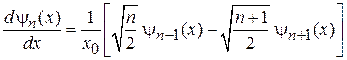. (3.35)

Матричные элементы координаты и импульса являются измеримыми величинами

,

.

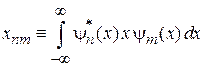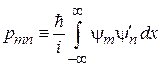Используя (3.33–35), находим

, ,

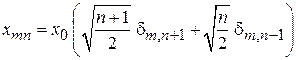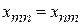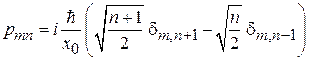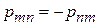, . (3.37)

Для средних значений и флуктуаций в состоянии n получаем

,

,

,

,

,

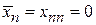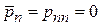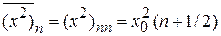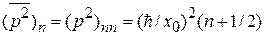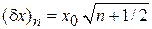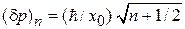.(3.38)

Энергия состояния. Из

, ,

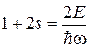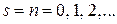получаем

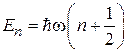. (3.39)

Спектр эквидистантный, расстояние между соседними уровнями

.

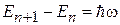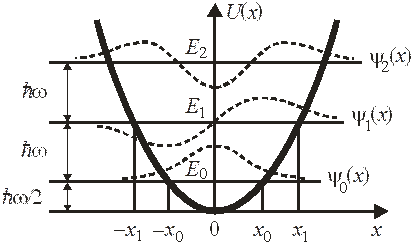
Номер квантового состояния n равен числу квантов энергии 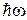, связанных с осциллятором. Переход к соседнему состоянию добавляет или удаляет квант энергии. Энергия основного состояния

.

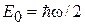Отсутствие состояния покоя у пространственно ограниченной системы следует из соотношения неопределенностей Гейзенберга.

Date: 2015-05-19; view: 834; Нарушение авторских прав