Примеры

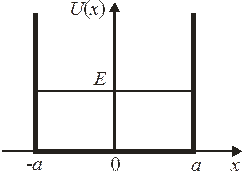
1. Найти состояния в прямоугольной симметричной потенциальной яме шириной 2 а с абсолютно непроницаемыми стенками 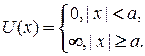Яма моделирует находящийся в вакууме кусок металла размером 2 a с большой работой выхода для свободного электрона.

Уравнение и решения. Внутри ямы при 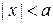уравнение Шредингера (3.2) имеет вид

,

где

, .

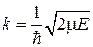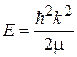Яма симметричная, используем вещественные четное и нечетное решения

,

.

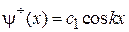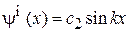Граничные условия. При 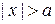потенциальная энергия бесконечная, выполняется граничное условие (3.14) – за пределами ямы и на стенках волновая функция равна нулю. При 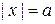находятся узлы волновой функции

,

.

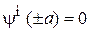Четные состояния. Граничное условие дает

.

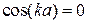Получаем дискретный набор решений ,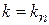

,

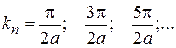в общем виде

,

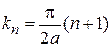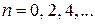
Тогда

,

.

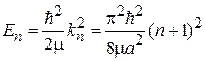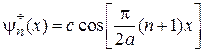Находим с из условия ортонормированности

.

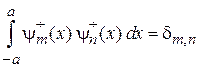С учетом

,

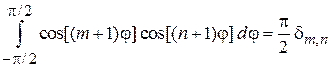с точностью до постоянной фазы получаем ,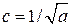

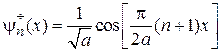. (П.3.1)

Основное состояние

,

.

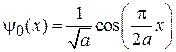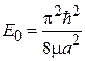Нечетные состояния. Условие

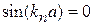
дает набор решений

,

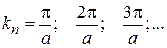в общем виде

,

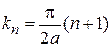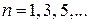
Тогда

,

.

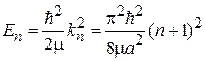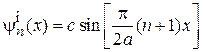Ортонормированность

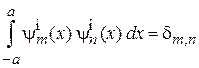
дает ,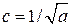

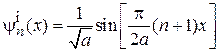. (П.3.2)

Первое возбужденное состояние

,

.

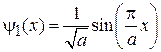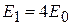Объединяя результаты для четных и нечетных состояний, получаем спектр энергии

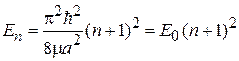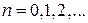, , (П.3.3)

где n – число узлов волновой функции. Энергии четных и нечетных состояний чередуются. Расстояние между соседними уровнями увеличивается с ростом n как 2 n +1.

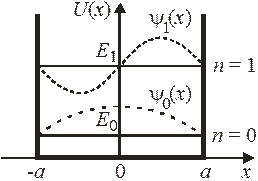
Функции состояний образуют ортонормированный базис

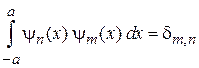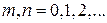, (П.3.4)

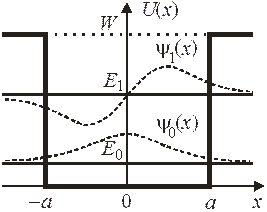
2. Найти связанные состояния в прямоугольной яме глубиной W и шириной .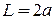

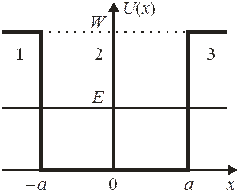
Такая яма существует в гетероструктуре 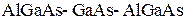. Слой 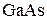имеет узкую запрещенную зону по сравнению с соседними слоями. В зоне проводимости образуется прямоугольная потенциальная яма глубиной 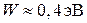, шириной 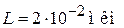. На дне зоны проводимости 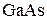эффективная масса электрона .

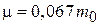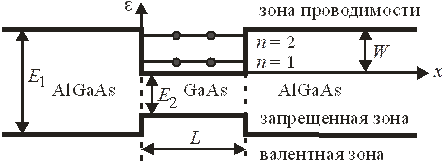
Вдоль оси x выделяем участки 1, 2 и 3. Внутри ямы в области 2 при 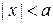учитываем 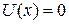. Ищем связанные состояния 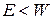. Используем уравнение Шредингера (3.2)

,

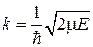. (П.3.6)

Яма симметричная, выделяем четное и нечетное решения

,

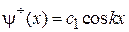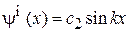. (П.3.7)

Вне ямы в областях 1 и 3 при 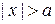учитываем 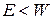, уравнение Шредингера (3.1)

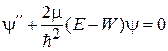
получает вид

,

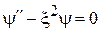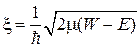. (П.3.8)

Используем убывающие с удалением от ямы решения

, ,

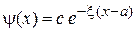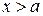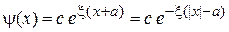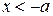, . (П.3.9)

Параметры 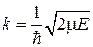и 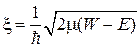связаны соотношением

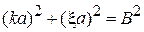, (П.3.10)

где

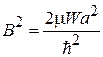
не зависит от E.

Сшиваем решения при 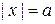, используя (3.11) и (3.12)

,

.

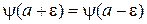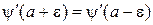Для четного решения сшивание

,

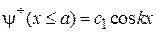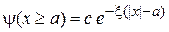
дает

,

.

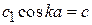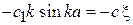Взаимным делением избавляемся от постоянных с и 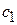. Получаем трансцендентное уравнение

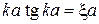. (П.3.11)

Для нечетного решения сшиваем

, ,

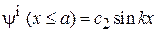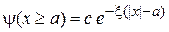аналогично получаем

,

,

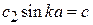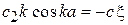тогда

. (П.3.12)

Для нахождения k и ξ для четных состояний используем систему уравнений (П.3.10) и (П.3.11)

,

.

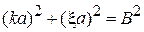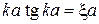Для нечетных состояний используем (П.3.10) и (П.3.12)

,

.

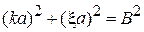Уравнения трансцендентные, для их решения применяем графический метод. Рассматриваем безразмерные 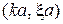как декартовые координаты на плоскости. Уравнение

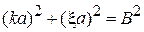
дает окружность. Радиус

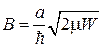
выражается через данные задачи. На рис. дуги 1, 2, 3 соответствуют разной глубине ямы. Функци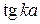и и 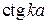периодические, каждой ветви 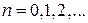соответствует своя кривая. Уравнение

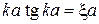
для ветвей 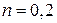соответствует пунктирным кривым. Уравнение

при 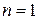дает сплошную кривую.

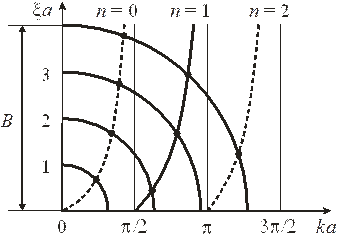
Точка пересечения окружности с кривой, спроектированная на оси координат, дает 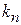и , и 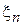уровень энергии

.

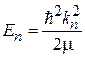При малой глубине ямы W радиус окружности 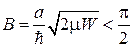(на рис. дуга 1). Согласно рисунку в одномерной яме сколь угодно малой глубины существует связанное основное состояние 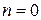. При любой глубине ямы основное состояние удовлетворяет

, ,

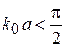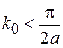тогда для 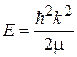получаем 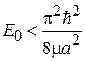, где 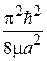– энергия основного состояния в бесконечно глубокой яме шириной 2 a. Энергия основного состояния Е ₀ в яме конечной глубины меньше энергии основного состояния в бесконечно глубокой яме.

С увеличением глубины ямы растет радиус окружности 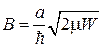, согласно рисунку возрастает 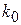и энергия основного состояния. При 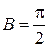, 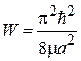появляется следующий уровень с 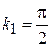и энергией 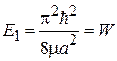у верха ямы. При дальнейшем увеличении W возрастают 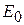и 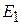, но медленнее, чем W. В интервале

,

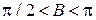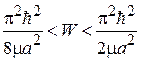
существуют два состояния – основное и первое возбужденное.

3. Найти связанные состояния в дельта-образной яме , где – безразмерный параметр, d – параметр с размерностью длины.

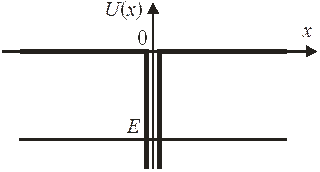
Для связанного состояния с 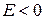из (3.1)

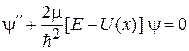
получаем

,

, .

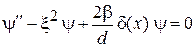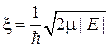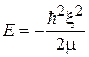При 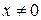уравнение

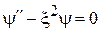
дает убывающие на бесконечностях решения

,

.

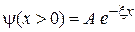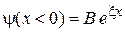Сшиваем их при 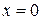, используя (3.11) и (3.13):

, ,

,

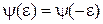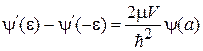где

, .

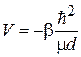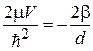Находим

,

,

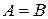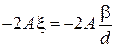тогда

,

,

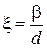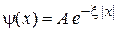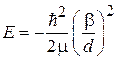. (П.3.15)

Существует лишь одно связанное состояние. Условие нормировки

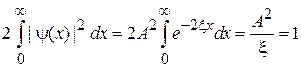
дает

,

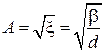в результате

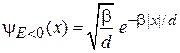. (П.3.16)

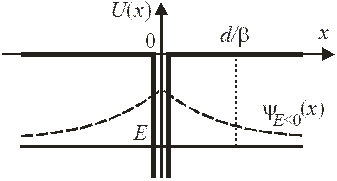
Функция уменьшается в е раз при 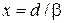. Чем больше β, тем выше уровень энергии и быстрее убывает 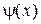при удалении от ямы.

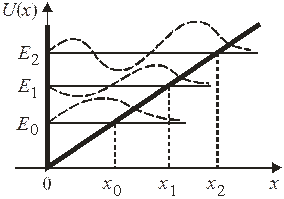
4. Найти уровни энергии в треугольной яме 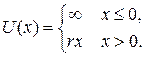Линейная зависимость потенциала создается однородным электрическим полем плоского конденсатора, в котором находится заряд q, тогда 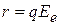. Обкладки конденсатора расположены перпендикулярно оси x.

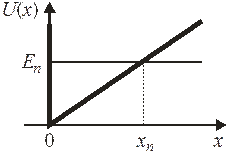
Пространственное ограничение для частицы приводит к дискретности ее спектра энергии. Частица с полной энергией 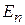имеет кинетическую энергию

, .

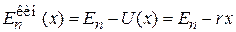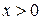На границе классического движения 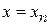частица останавливается,

.

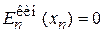Координата точки остановки

.

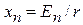В уравнении Шредингера (3.1)

, ,

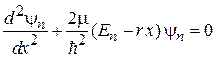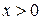переходим к безразмерному аргументу z, который отсчитываем от точки остановки:

.

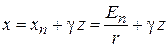Параметр γ с размерностью длины выбираем из условия

,

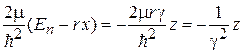находим

.

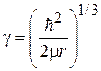В результате после замены

, ,

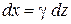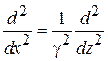уравнение Шредингера становится уравнением Эйри

.

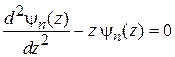Решение имеет вид интеграла Эйри

. (П.3.27)

Спектр энергии получаем из краевого условия (3.14) на непроницаемой стенке ,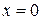

.

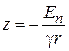
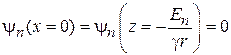Подставляем (П.3.27)

.

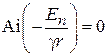Используем корни функции Эйри :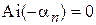

, , , , ,...,

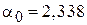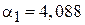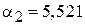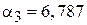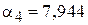находим спектр энергии

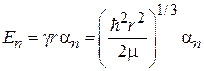. (П.3.28)

С ростом n расстояние между соседними уровнями медленно уменьшается. Для основного состояния

.

Date: 2015-05-19; view: 2155; Нарушение авторских прав