Среднее значение

Дискретный спектр. Нормировка (1.16) и ортогональность (2.16) дают условие ортонормированности

, (2.21)

где 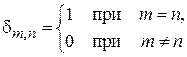– символ Кронекера. Нормировка 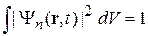требует достаточно быстрого убывания плотности вероятности за пределами некоторого конечного объема. Следовательно, дискретный спектр соответствует связанному состоянию.

Непрерывный спектр. Если индекс собственной функции принимает непрерывные значения, то в (2.21) вместо символа Кронекера ставится дельта-функция

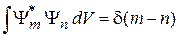. (2.22)

При 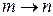интеграл стремится в бесконечность. Плотность вероятности 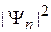конечна и не равна нулю за пределами любого конечного объема. Следовательно, непрерывный спектр соответствует неограниченному движению.

Разложение функции по ортонормированному базису оператора .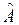

Дискретный спектр

. (2.23)

Непрерывный спектр

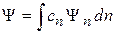. (2.24)

В этих состояниях физическая величина, описываемая оператором 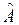, не имеет определенного значения.

Коэффициенты разложения 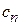. Умножаем (2.23) или (2.24) на 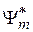, интегрируем по пространственным переменным, учитываем условия ортонормированности (2.21) или (2.22). Для дискретного и непрерывного спектров находим

. (2.25)

Для дискретного спектра подставляем (2.23) в условие нормировки (1.16)

.

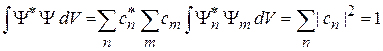Сравниваем результат с нормировкой вероятности дискретных событий

,

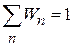тогда вероятность обнаружения состояния 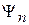в нормированном состоянии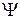

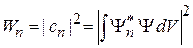. (2.26)

Для непрерывного спектра из (1.16), (2.24) и (2.22)

.

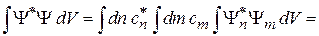
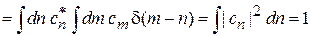Сравниваем результат с нормировкой вероятности непрерывных событий

,

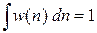тогда плотность вероятности обнаружения состояния 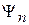в нормированном состоянии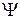

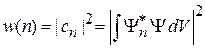. (2.27)

Среднее значение величины, описываемой оператором 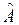в нормированном состоянии 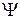, равно

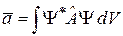. (2.28)

Доказательство:

Разлагаем состояние по собственным функциям оператора с дискретным спектром и подставляем в (2.28)

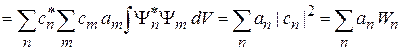
– определение среднего дискретной величины.

Для непрерывной величины аналогично находим

.

Date: 2015-05-19; view: 465; Нарушение авторских прав