Заряд в магнитном поле. Магнитное поле изменяет фазу волновой функции заряда, длину волны де Бройля и условие квантования

Магнитное поле изменяет фазу волновой функции заряда, длину волны де Бройля и условие квантования. В соотношении (1.13) 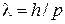механический импульс p заменяется полным импульсом P, сохраняющимся в магнитном поле.

Полный импульс. Механический импульс 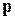заряда q в электрическом поле E изменяется согласно второму закону Ньютона 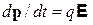. Интегрирование дает

.

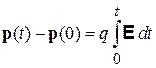Пусть электрическое поле создается магнитным полем 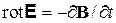благодаря явлению электромагнитной индукции. Используем 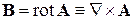, где А – векторный потенциал, и получаем 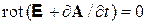. Учитываем , где f – произвольная скалярная функция, и находим . Векторный потенциал не является измеримой величиной в классической электродинамике, его выбор не однозначен. Калибровка 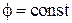дает поле Фарадея , изменяющее импульс:

.

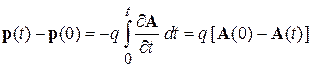В результате сохраняется полный импульс

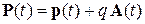, (1.20)

складывающийся из механического импульса частицы 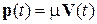и импульса магнитного поля 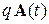, в котором находится заряд.

Квантование в магнитном поле. Фаза волновой функции и длина волны де Бройля определяются полным импульсом.

Из (1.17) и (1.20)

,

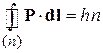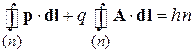. (1.21)

По теореме Стокса

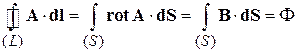
– циркуляция векторного потенциала A по замкнутому контуру L равна потоку Ф вектора индукции B через площадь S, ограниченную контуром L, где направления dl и dS связаны правилом правого винта.

Если положительный заряд q удерживается на круговой траектории n силой Лоренца 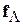, как показано на рис. 1.2, то направление его перемещения dl связано с полем B правилом левого винта, тогда

.

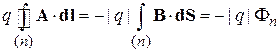Подстановка в (1.21) дает для траектории n условие квантования

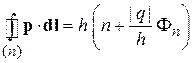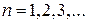, (1.22)

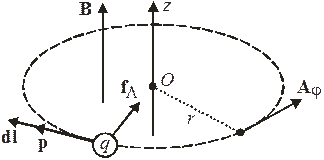
Рис. 1.2. Заряд 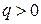в магнитном поле

Date: 2015-05-19; view: 410; Нарушение авторских прав