Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Значения операторА
|
|
Собственная функция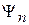 
оператора 
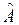удовлетворяет уравнению
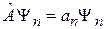, (2.8)
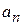– собственное значение оператора.
Если система находится в состоянии 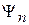, то измерение величины a, описываемой оператором 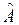, дает однозначный результат 
.
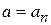Спектр оператора – множество его собственных значений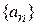 
.
Если 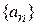счетное, то спектр дискретный.
Если 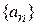образует непрерывный набор, то спектр непрерывный.
Если k разных собственных функций имеют одинаковые собственные значения, то спектр k- кратно вырожден.
Коммутирующие операторы имеют одинаковый набор собственных функций, соответствующие физические величины одновременно имеют определенные значения.
Доказательство:
Пусть 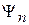– собственная функция 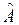, тогда
, 
.
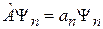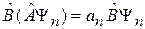Из коммутативности
,
тогда
.
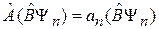Следовательно,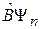 
– собственная функция 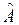, пропорциональная :
.
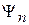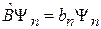В результате 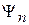– собственная функция 
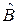с собственным значением 
.
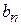Оператор координаты. Пусть 
– собственная функция с собственным значением 
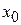, тогда
.
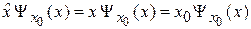Сравниваем с фильтрующим свойством дельта-функции
,
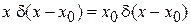находим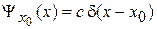 
. Условие нормировки дает 
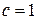, тогда
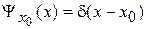. (2.9)
Функция равна нулю во всех точках, кроме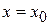 
.
x 0 – любое вещественное число, спектр непрерывный.
Date: 2015-05-19; view: 415; Нарушение авторских прав