Физических величин с не коммутирующими операторами

Рассмотрим две физические величины А и В, коммутатор операторов которых отличен от нуля: 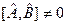. Докажем теорему.

Теорема: Если операторы и 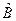не коммутируют, то произведение дисперсий соответствующих физических величин не меньше четверти квадрата модуля среднего значения коммутатора их операторов 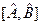, т.е. .

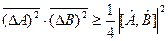Доказательство: Введем в рассмотрение операторы

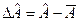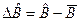, , (12.1)

и примем во внимание, что статистический разброс значений физических величин определяется дисперсией:

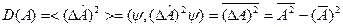
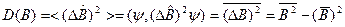, (12.2)

где 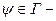произвольный вектор состояния квантовой системы. Для определения связи с дисперсий (12.2) рассмотрим векторы гильбертова пространства

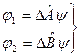(12.3)

Согласно неравенству Буняковского-Коши, которое справедливо и в гильбертовом пространстве, можно записать:

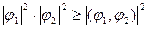(12.4)

где

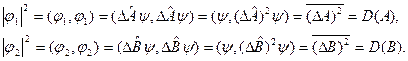(12.5)

В преобразованиях (12.5) учтена эрмитовость операторов 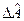и 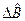. Квадрат модуля скалярного произведения векторов 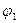и 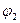преобразуется к виду:

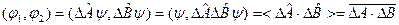(12.6)

Тогда неравенство (12.4) примет вид:

(12.7)

Для определения среднего значения 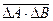преобразуем оператор :

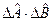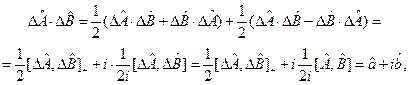(12.8)

где 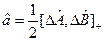и 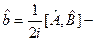эрмитовы операторы. На основе (12.8) находим:

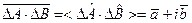(12.9)

подставляя (12.9) в неравенство (12.7), получим 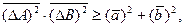откуда тем более справедливо неравенство

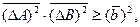т.е. 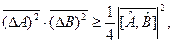(12.10)

что и требовалось доказать: произведение дисперсий физических величин А и В с некоммутирующими операторами не меньше четверти квадрата модуля среднего значения коммутатора этих операторов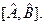

Извлекая корень квадратный из соотношения (12.10), получим:

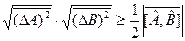. (12.11)

Обычно для упрощения записи это неравенство записывается в виде:

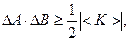(12.12)

где .

Для случая, когда 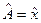, , 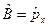выражение (12.12) дает ранее полученное соотношение неопределенностей (11.13’).

Итак, соотношения неопределенностей, которые существуют между некоторыми физическими величинами, полностью определяются коммутаторами этих операторов этих величин.

Отсюда, в частности, следует вывод, что если операторы физических величин попарно коммутируют друг с другом, то эти физические величины могут одновременно иметь определенные значения. Это условие одновременной измеримости физических величин доказано в §9.

Физическая сущность соотношений неопределенностей состоит в том, что для квантовых систем, в отличие от классических, не имеет смысла требовать одновременно определенных значений всех физических величин, что обусловлено двойственной природой объектов микромира. Существование соотношений неопределенностей для физических величин в квантовой механике обусловлено не какими-то особенностями измерения, а внутренними особенностями самих квантовых систем.

Таким образом, соотношения неопределенностей являются математическим выражением наличия у частиц (микрообъектов) как корпускулярных, так и волновых свойств.

Date: 2015-05-18; view: 609; Нарушение авторских прав