Шредингеровская картина движения. Волновое уравнение Шредингера

Э.Шредингер в 1926 г. записал свое квантовое уравнение движения, считая, что с течением времени меняется вектор состояния системы ψ(t), а операторы динамических переменных не зависят от времени: . Эта картина эволюции квантовой системы во времени получила название шредингеровской картины движения.Какому же уравнению удовлетворяет вектор состояния, т.е. каков вид основного уравнения квантовой динамики в шредингеровском представлении^[9]?

Для ответа на этот вопрос воспользуемся формулой среднего значения динамической переменной в представлении Гейзенберга:

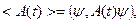(14.1)

где

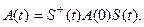(13.24)

Тогда выражение (14.1) преобразуется к виду:

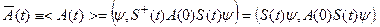(14.2)

где унитарный оператор 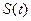, действуя на вектор состояния, переносит на него временную эволюцию квантовой системы:

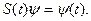(14.3)

Таким образом, в шредингеровском представлении вектор состояния квантовой системы со временем меняется согласно закону:

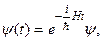(14.4)

операторы же остаются неизменными: .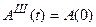

Следовательно, связь между гейзенберговской и шредингеровской картинами развития системы во времени осуществляется унитарным преобразованием, производимым с помощью оператора эволюции S(t) (13.20).

Дифференцируя по времени выражение (14.4), получим квантовомеханическое уравнение движения Шредингера:

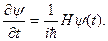(14.5)

В координатном представлении вектор состояния переходит в волновую функцию 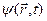, а уравнение (14.5) приобретает вид известного волнового уравнения квантовой динамики:

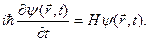(14.6)

Гамильтониан H, например, для квантовой частицы с массой m₀, движущейся в потенциальном поле, имеет вид (6.27):

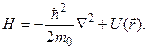
Date: 2015-05-18; view: 502; Нарушение авторских прав