Глава V. Квантовая динамика. Эволюция квантовых систем во времени

Уравнения движения составляют основу физической теории. Так в классической механике состояние системы описывается каноническими переменными q_j, p_j, число которых равно удвоенному числу степеней свободы. Все другие физические величины являются функциями канонических переменных. Зависимость этих переменных от времени q_j=q_i(t), p_j=p_j(t) есть одновременно эволюция во времени и состояние классической системы, и всех физических величин.

Рассмотрим особенности квантовой динамики, учитывая, что состояние квантовой системы описывается вектором ψ 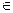Г, физические же величины изображаются линейными самосопряженными операторами.

Что же должно изменяться с течением времени в процессе эволюции квантовой системы?

Ответить однозначно на этот вопрос нельзя, поскольку существуют различные способы описания эволюции квантовых систем во времени. Так в 1925 г. В.Гейзенберг записал знаменитое уравнение эволюции во времени эрмитовых операторов физических величин, характеризующих квантовую систему, при этом полагалось, что вектор состояния во времени не меняется, т.е. ψ(t)=ψ(0)=ψ - гейзенберговская картина движения. Уравнение Гейзенберга было первоначально введено в матричной форме, тем самым было положено начало направлению, которое получило название "матричной механики". В 1926г. появилось уравнение Шредингера для волновой функции ψ(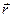,t), описывающее эволюцию во времени состояния квантовой системы. Операторы же физических величин при этом не зависят от времени: 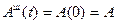. Такова картина движения Шредингера, который положил начало направлению, получившему название "волновой механики".

В 1927 г. П.Дирак показал эквивалентность уравнений Гейзенберга и Шредингера.

§13. Эволюция квантовой системы во времени: уравнение Гейзенберга

В классической механике при отыскании первых интегралов движения важное значение имеют скобки Пуассона. Дело в том, что выражение полной производной по времени от некоторой функции канонических переменных и времени имеет вид:

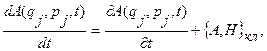(13.1)

где

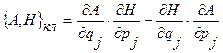(13.2)

называются скобками Пуассона, 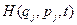- функция Гамильтона.

Уравнение (13.1) выражает эволюцию классической системы во времени. Действительно, если выбирать в качестве физической величины А канонические переменные q_j, p_j, то легко получить уравнения движения Гамильтона:

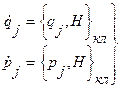(13.3)

Согласно 4-му постулату квантовой механики каждой физической величине (динамической переменной) ставится в соответствие линейный эрмитов оператор:

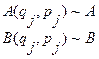
Следовательно, классическим скобкам Пуассона

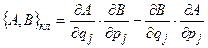(13.2`)

должны быть поставлены в соответствие квантовые скобки 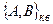, вид которых определен Дираком из следующих соображений.

Если A=x, B=p_x, то 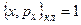. Тогда с учетом коммутатора операторов x и p_x (10.4) можно получить аналогичное квантовое выражение, равное единице:

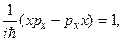(13.4)

т.е. квантовые скобки для операторов величин x и p_x должны иметь вид:

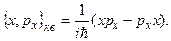(13.5)

Таким образом, классическим скобкам соответствуют квантовые скобки Пуассона:

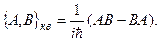(13.6)

Тогда в силу принципа соответствия классическому уравнению (13.1), выражающему временную эволюцию системы, следует сопоставить квантовое уравнение движения:

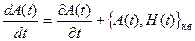(13.7)

Это и есть уравнение Гейзенберга, при этом система описывается не меняющимся с течением времени вектором ψ: ψ(0)=ψ(t)=ψ. Эволюция квантовой системы связана с тем, что от времени зависят операторы всех физических величин согласно уравнению (13.7), вектор же состояния системы не зависит от времени - гейзенберговская картина движения (гейзенберговское представление).

Выбирая в качестве A операторы координат и импульса, которые явно не зависят от времени, из уравнения (13.7) получим квантовые канонические уравнения движения - уравнения Гамильтона:

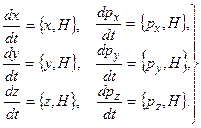(13.8)

Получим строгое решение уравнения Гейзенберга для случая, когда 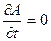и 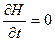. Если A и H явно не зависят от времени, то квантовое уравнение движения (13.7) принимает вид:

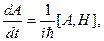(13.9)

причем 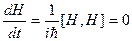, т.е. оператор полной энергии не зависит от времени: H(t)=H(0)=H. Тогда уравнение (13.9) упрощается:

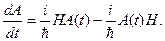(13.10)

Для определения вида решения уравнения (13.10) учтем лишь пока первое слагаемое в правой части, т.е. рассмотрим уравнение

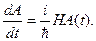(13.11)

Решением этого уравнения является оператор

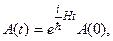(13.12)

где экспоненту можно представить разложением в ряд:

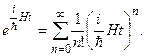(13.13)

Тогда решение уравнения (13.10) будем искать в виде:

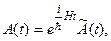(13.14)

здесь 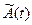учитывает наличие второго слагаемого в правой части уравнения (13.10).

Потребуем, чтобы (13.14) было решением уравнения (13.10). Для этого вычислим :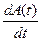

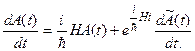(13.15)

Подставив (13.14) и (13.15) в уравнение (13.10), найдем:

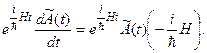(13.16)

Отсюда для искомого оператора 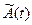получаем уравнение:

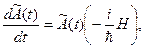(13.17)

решением которого является оператор

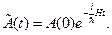(13.18)

Следовательно, оператор любой физической величины меняется со временем по закону:

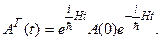(13.19)

Этот закон можно записать через унитарные операторы. Для этого введем в рассмотрение оператор

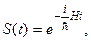(13.20)

называемый оператором эволюции системы во времени. Тогда обратным ему оператором будет

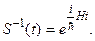(13.21)

Учитывая эрмитовость гамильтониана H, найдем оператор 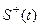, сопряженный оператору (13.20):

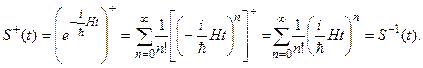^[8]

Итак,

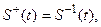(13.22)

тогда

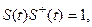(13.23)

т.е. оператор эволюции системы 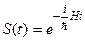является унитарным оператором.

Таким образом, связь оператора Гейзенберга 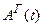с 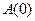осуществляется унитарным преобразованием:

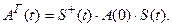(13.24)

Date: 2015-05-18; view: 980; Нарушение авторских прав