О возможности одновременно точного определения динамических переменных (наблюдаемых)

В классической механике частицу в каждый момент времени характеризуют определенными значениями координат и проекциями импульсов.

В квантовой же механике дело обстоит иным образом. Для этого рассмотрим одномерное движение частицы вдоль оси OX с заданным импульсом 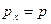, состояние которой описывается в координатном представлении волновой функцией (6.17):

.

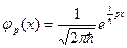Вероятность измерения координаты в этом состоянии определяется плотностью вероятности 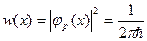. Таким образом, все значения координаты у частицы в этом состоянии 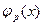оказываются равновероятными.

Если же иметь состояние с определенным значением координаты 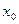, которое описывается волновой функцией в импульсном представлении (7.11):

,

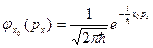то в этом случае равновероятными оказываются все значения импульса 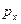: 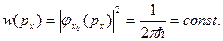Из приведенных примеров следует, что в квантовой области не существует таких состояний частиц, в которых импульс и сопряженная ему координата одновременно имели бы определенные значения. В таком же взаимоисключающем положении находятся и многие другие величины.

Таким образом, в квантовой механике некоторые физические величины не могут иметь определенных значений в одном и том же состоянии системы, т.е. эти величины не могут быть одновременно измеримы. В связи с этим необходимо вывести условие одновременной измеримости физических величин.

Согласно четвертому постулату квантовой механики каждой физической величине 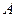сопоставляется линейный эрмитов оператор : 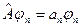. Динамическая переменная 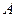имеет в состоянии 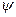определенное значение, если вектор состояния совпадает с одним из собственных векторов оператора , т.е. если 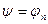, то физическая величина 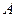в этом состоянии имеет значение .

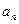Пусть собственный вектор 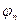оператора является одновременно собственным вектором и оператора 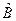, тогда этот вектор удобно записать в виде 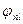, т.к.

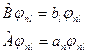
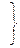(9.1)

Такой вектор состояния 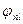называется общим собственным вектором операторов и 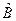и описывает такое состояние, в котором функции величин А и В имеют определенное значение. Если система общих собственных векторов 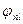операторов и 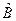является полной, тогда любой вектор состояния можно представить в виде суперпозиции:

,

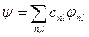где квадраты коэффициентов разложения 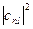определяют вероятность получения определенных значени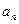й и 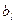при измерении физических величин 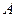и . В этом случае говорят, что физические величины 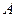и в принципе одновременно измеримы, что реализуется в случае, когда вектор состояния 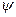совпадает с одним из собственных векторов 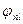. Следовательно, динамические переменные 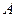и одновременно измеримы, если их операторы и 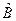имеют общую полную систему собственных векторов.

Date: 2015-05-18; view: 428; Нарушение авторских прав