Условие возможности одновременного измерения двух физических величин

Для решения поставленного вопроса докажем теорему:

Теорема: Для того, чтобы физические величины 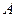и были в принципе одновременно измеримы, необходимо и достаточно равенства нулю коммутатора операторов и 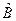этих величин, т.е. .

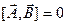Доказательство: Пусть физические величины 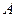и могут быть одновременно измерены, т.е. операторы и 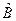имеют общую полную систему собственных векторов 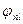. Докажем, что коммутатор операторов и 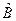равен нулю: .

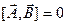Разложим любой вектор 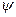состояния квантовой системы по общей полной системе собственных векторов :

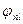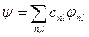. (9.2)

Вычислим результат действия оператора 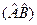на вектор (9.2):

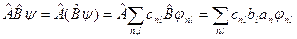. (9.3)

Затем вычислим результат действия 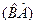на :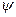

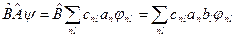. (9.4)

Из равенства правых частей в выражениях (9.3) и (9.4) следует:

,

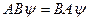где 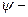произвольный вектор. Таким образом,

,

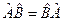т.е.:

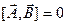. (9.5)

Доказательство достаточности условия (9.5).

Докажем, что если операторы и 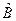коммутируют друг с другом, то соответствующие физические величины 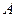и в принципе одновременно измеримы, т.е. операторы и 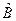имеют общую полную систему собственных векторов .

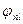Предварительно докажем лемму:

Лемма: Если 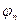есть собственные векторы оператора с собственными значениями 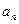(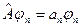), и оператор коммутирует с оператором 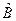, т.е. 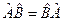, то векторы 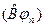также являются собственными векторами , принадлежащими тем же собственным значениям 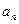, т.е.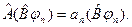

Доказательство: В этом легко убедиться, вычислив результат действия на векторы :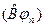

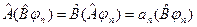. (9.6)

При доказательстве достаточности условия (9.5) рассмотрим два случая.

1) Случай отсутствия вырождения собственных значений 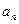оператора .

По условию каждому значению 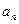принадлежит один собственный вектор, описывающий одно и только одно квантовое состояние: 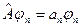. С учетом леммы: 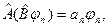откуда следует, что векторы 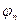и 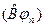, описывая одно и то же состояние, могут отличаться друг от друга лишь постоянным множителем:

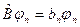. (9.7)

Значит, каждый собственный вектор 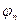является собственным для операторов и 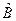, т.е. операторы и 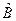имеют общую полную систему собственных векторов. Следовательно, физические величины 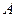и в принципе одновременно измеримы, если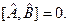

2) Случай наличия вырождения: собственному значению 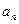принадлежит несколько собственных векторов оператора . В этом случае 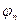и 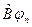могут и не совпадать.

Разложим вектор 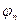по собственным векторам оператора :

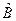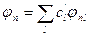, (9.8)

где 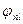определяются уравнением 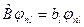. Преобразуем уравнение 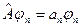с помощью разложения (9.8) к виду:

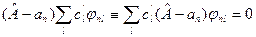. (9.9)

Согласно лемме

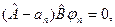(9.10)

Тогда с учетом разложения (9.8) уравнение (9.10) записывается в виде:

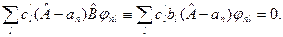(9.11)

В результате получаем систему уравнений:

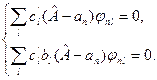(9.12)

Эта система уравнений совместима, если

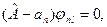(9.13)

откуда следует, что и и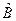меют общую полную систему векторов 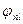, т.е. 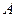и в принципе одновременно измеримы. Итак, если два оператора коммутируют, то они имеют общую полную систему собственных векторов, физические же величины, изображающиеся этими операторами, могут быть одновременно точно определены (измерены).

Date: 2015-05-18; view: 626; Нарушение авторских прав