Вывод соотношений неопределенностей для координат и канонически сопряженных импульсов

Физические величины, изображающиеся не коммутирующими операторами в рамках квантовой механики не могут быть одновременно определены (изменены). Наиболее важным является в этом случае вычисление отклонений значений таких величин от средних значений их операторов.

Вычислим отклонение от средних значений операторов двух канонически сопряженных величин: координаты и импульса 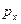. Для этого ради простоты рассмотрим одномерный стационарный случай движения частицы вдоль оси OX. Тогда средние значения координаты и импульса в координатном представлении могут быть найдены соответственно из соотношений:

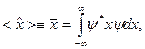(11.1)

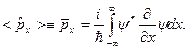(11.2)

Разброс значений величин около их средних значений характеризуется дисперсией или среднеквадратичным отклонением:

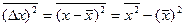(11.3)

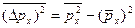(11.4)

Без ограничения общности доказательства можно выбрать систему координат с началом в центре волнового пакета (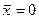), причем так, что система координат движется с ним (). В этом случае будем иметь:

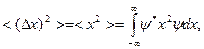(11.5)

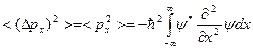(11.6)

Для нахождения связи между 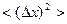и 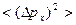рассмотрим интеграл:

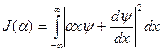, (11.7)

где 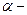некоторая вещественная переменная величина, не зависящая от . Выражение (11.7) можно представить в виде неотрицательного трехчлена:

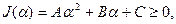(11.8)

где

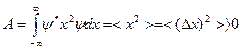, (11.9)

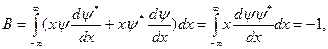(11.10)

(11.11)

интегралы в (11.10) и (11.11) вычислены по частям и при этом учтены стандартные условия (а именно, конечность), наложенные на волновые функции.

Условие 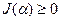при 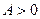на основании теоремы о корнях квадратного уравнения принимает вид:

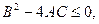(11.12)

откуда 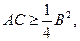т.е.

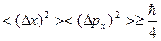(11.13)

Это неравенство представляет строгую формулировку соотношения неопределенностей для координаты и импульса 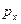. Извлекая квадратный корень из обеих частей неравенства (11.13), получим:

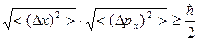(11.13’)

Аналогичные соотношения неопределенностей имеют место для координат y, z и сопряженных для них импульсов .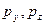

Таким образом, соотношения неопределенностей Гейзенберга для координат и канонически сопряженных импульсов имеют вид:

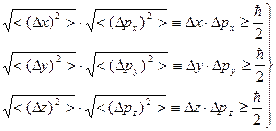(11.14)

Соотношения (11.14) показывают, что координаты и сопряженные импульсы не могут быть одновременно точно измерены, и что минимально возможная величина произведения дисперсий измеряемых координаты () и импульса (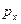) ограничены постоянной Планка. Это ограничение связано не с методикой измерения, но обусловлено наличием корпускулярно-волновой природы квантовых объектов.

Соотношения неопределенностей (11.14) являются и рабочим инструментом в квантовой механике, позволяя проводить важные количественные оценки: энергии основного состояния атома водорода, минимально возможной энергии у частиц в потенциальных ямах; ответить на вопросы такого типа: могут ли быть электроны в составе атомного ядра и т.д.

В качестве примера подобного использования соотношений неопределенностей оценим минимальную энергию колебаний линейного гармонического осциллятора (ЛГО).

Из классического выражения для энергии ЛГО

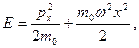(11.15)

где 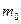и 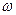- масса и собственная частота осциллятора, следует, что энергия будет минимальной, когда значения и 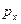минимальны, но 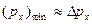; 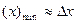. Поэтому из соотношений неопределенностей (11.14) следует связь минимальных значений координаты и импульса: 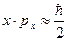. Подставляя 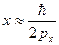в формулу энергии ЛГО, получим

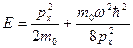(11.16)

Исследуя выражение (11.16) на экстремум (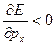), находим 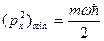. Следовательно, минимальная энергия ЛГО оказывается равной:

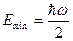, (11.17)

это так называемая энергия нулевых колебаний осциллятора, отличие ее от нуля иллюстрирует принципиально общее положение квантовой механики: нельзя реализовать микрообъект на «дне потенциальной ямы», причем этот вывод не зависит от вида потенциальной ямы, т.к. является прямым следствием соотношений неопределенностей.

Date: 2015-05-18; view: 1114; Нарушение авторских прав