Квантовых систем во времени

При сопоставлении рассмотренных картин эволюции прежде всего следует заметить, что если в начальный момент времени t₀=0 в координатном представлении имеем 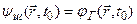и 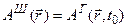, т.е. совпадают как волновые функции, так и операторы физических величин в картинах движения Шредингера и Гейзенберга, то в последующие моменты времени обнаруживаются две различные ситуации: в представлении Шредингера зависимость от времени перенесена на волновую функцию 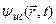, а в представлении Гейзенберга - на операторы .

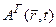Эквивалентность обоих методов описания следует и из равенства матричных элементов эрмитовых операторов в шредингеровской и гейзенберговской картинах временной эволюции.

Действительно, в картине эволюции Шредингера в координатном представлении матричный элемент оператора A для любых двух состояний и равен:

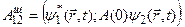(15.4)

Используя унитарное преобразование (14.4), запишем

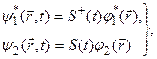(15.5)

где 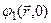и 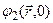- волновые функции соответственно тех же двух состояний в гейзенберговской картине эволюции системы во времени.

С учетом выражений (15.5) матричный элемент (15.4) преобразуется к виду:

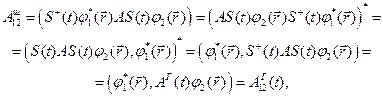(15.6)

т.е.

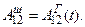(15.6`)

Матричные элементы операторов определяют физически наблюдаемые величины, поэтому не могут быть различными в эквивалентных представлениях (о чем свидетельствует вывод уравнения (14.5)). Другими словами, физические результаты должны входить в математический аппарат квантовой механики как унитарные инварианты.

Таким образом, требование унитарной инвариантности соответствующих результатов может служить дополнительным критерием правильности сформулированных ранее (глава 2, §5) основных постулатов (аксиом), положенных в основу квантовой механики.

Гейзенберговская картина эволюции обладает тем преимуществом, что позволяет выявить математическую аналогию квантовой механики и классической механики. Именно в представлении Гейзенберга квантовомеханические соотношения имеют вид классических соотношений, в которых физические величины заменены соответствующими операторами. Особенно широко применяется гейзенберговское представление в квантовой теории поля.

Для практических расчетов удобнее всего пользоваться шредингеровской картиной эволюции, в которой операторы A, сопоставляемые классическим динамическим переменным, не зависят от времени. Всю информацию о временном развитии системы несет волновая функция 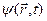, удовлетворяющая волновому уравнению Шредингера (14.6). В большинстве случаев решить дифференциальное уравнение (14.6) значительно легче, чем найти решение матричных уравнений Гейзенберга.

Помимо гейзенберговского и шредингеровского представлений часто применяется представление взаимодействия, введенное Дираком. В представлении Дирака в общем случае операторы и векторы состояний явно зависят от времени.

Это представление удобно, когда в гамильтониане H задачи можно выделить малую часть V так, что

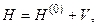(15.7)

где 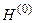не зависит от времени; оператор V, называемый оператором возмущения, может зависеть и от времени.

В конкретных расчетах оператор 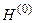описывает, например, систему невзаимодействующих частиц (электронов в атоме гелия), а оператор V учитывает их взаимодействие. Это представление очень удобно при использовании одного из приближенных методов квантовой механики - теории возмущений (стационарной, когда 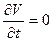, и нестационарной - 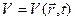). Очень часто представление взаимодействия используется в квантовой электродинамике.

Наиболее же общая форма описания состояния квантовых систем (гейзенберговская картина эволюции) основана на использовании оператора матрицы плотности , удовлетворяющего уравнению фон Неймана (15.3). Преимущество этого метода описания состоит в единообразном рассмотрении чистых и смешанных состояний квантовых систем.

Date: 2015-05-18; view: 435; Нарушение авторских прав