Операторы физических величин в матричном представлении

Пусть в результате действия эрмитова оператора на вектор Y получается вектор c:

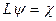. (8.7)

Разложим векторы y и c по базисным векторам 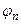уравнения (8.1):

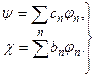(8.8)

Подставив выражение (8.8) в уравнение (8.7), умножим его затем скалярно на вектор :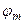

.

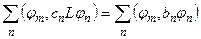Последнее равенство легко преобразуется к виду:

.

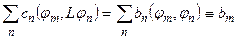Величину

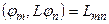(8.9)

называют матричным элементом оператора . Тогда уравнение (8.7) в «A – представлении» примет матричную форму:

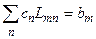. (8.10)

Совокупность матричных элементов 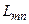полностью определяет оператор в матричном «A – представлении». Эту совокупность 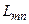можно представить в виде квадратной таблицы, имеющей бесконечное число строк и столбцов. У каждого матричного элемента первый индекс (m) означает номер строки, второй (n) – номер столбца. Эта таблица называется матрицей величины (оператора ):

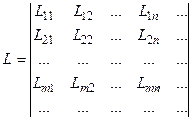. (8.11)

Вычислим матричные элементы оператора в своем собственном представлении, т.е. когда базисными векторами в разложении (8.8) являются собственные векторы 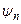оператора :

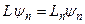. (8.12)

В этом случае

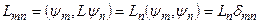, (8.13)

т.е. отличны от нуля лишь диагональные элементы матрицы. Таким образом, оператор в своем собственном представлении изображается диагональной матрицей:

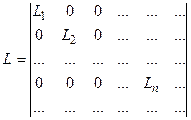, (8.11`)

в которой диагональные элементы совпадают с собственными значениями оператора .

Эрмитовость операторов, используемых в квантовой механике в матричной форме, выражается следующим образом:

,

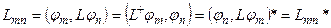т.е. матрица называется самосопряженной или эрмитовой, если

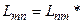. (8.14)

Матричное представление операторов легко обобщается на случай непрерывного спектра собственных значений. Для этого достаточно заменить суммы на интеграл и символ Кронекера-Вейерштрассе на d-функцию Дирака.

Так матричная запись оператора в координатном представлении (своем собственном) выглядит так:

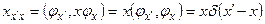. (8.15)

Подобным образом оператор может быть записан в матричной форме в «p – представлении»:

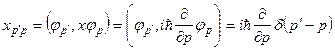. (8.16)

Date: 2015-05-18; view: 850; Нарушение авторских прав