Векторы состояния и операторы физических величин в импульсном представлении

И в импульсном представлении прежде всего надо найти явный вид операторов координат 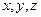и проекций импульсов .

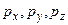Рассмотрим ради простоты одномерный случай: движение частицы вдоль оси Ox, тогда импульс ее 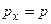изображается оператором 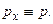Найдем явный вид оператора 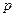в импульсном представлении. Для этого используем уравнение для собственных векторов и собственных значений оператора :

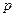(7.1)

Пусть в результате действия оператора 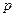на некоторый вектор 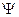гильбертова пространства получается другой вектор :

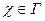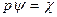. (7.2)

Воспользуемся Фурье-разложением векторов y и c по базисным векторам :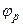

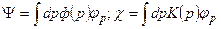, (7.3)

где

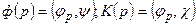. (7.4)

Тогда уравнение (7.2) приводится к виду:

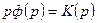. (7.5)

Подставляя (7.3) в уравнение (7.2), получим

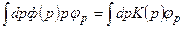, (7.6)

откуда с учетом (7.1) следует соотношение:

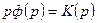. (7.7)

Из сравнения (7.7) и (7.5) находим явный вид оператора 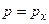в импульсном представлении:

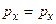. (7.8)

Аналогичным способом можно получить:

.

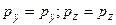Таким образом, в импульсном представлении

. (7.9)

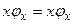Для определения явного вида оператора в импульсном представлении используем уравнение для собственных векторов и собственных значений этого оператора () в «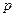 -представлении». Для этого разложим вектор 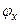в интеграл Фурье по базисным векторам :

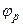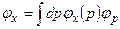, (7.10)

где коэффициенты разложения 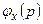, являясь собственными функциями оператора в импульсном представлении, вычисляются по формулам:

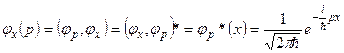(7.11)

(в преобразованиях учтены свойства скалярных произведений векторов унитарного пространства и формула (6.17)).

Уравнение для собственных функций и собственных значений оператора в импульсном представлении примет вид:

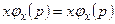. (7.12)

Если учесть выражение (7.11), то уравнение (7.12) выполняется для

. (7.13)

Рассмотрим обобщение полученного выражения оператора . Выбрав произвольный вектор 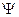, описывающий квантовое состояние частицы, разложим его по базисным векторам 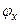в координатном представлении, а затем по 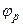в импульсном представлении:

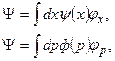
причем 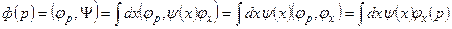– совокупность коэффициентов разложения есть Y–вектор в импульсном представлении, называемый волновой функцией в p–представлении. Тогда, если справедлива формула (7.13), то должно выполняться уравнение

.

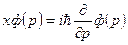И действительно,

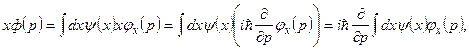
т.е.

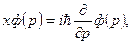
откуда получаем:

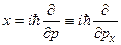. (7.14)

Итак, в импульсном представлении операторы координат имеют вид:

(7.15)

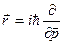. (7.16)

7.2. Средние значения физических величин в импульсном представлении (одномерный случай p=p_x)

В состоянии y квантовой системы среднее значение физических величин определяется по формуле (5.10) или по формуле (5.12), если норма вектора y не равна 1.

Если волновая функция 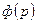удовлетворяет условию нормировки

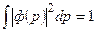, (7.17)

то для расчета среднего значения физической величины справедлива формула

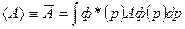, (7.18)

в частности,

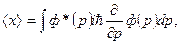(7.19)

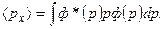(7.20)

§8. Матричное представление.

Date: 2015-05-18; view: 611; Нарушение авторских прав