Энергии в координатном представлении

На основе принципа соответствия по известному явному виду операторов канонических переменных (координат и проекций вектора импульса) легко записать явный вид оператора любой физической величины в том же представлении. Для этого в классическую формулу физической величины вместо координат и проекций импульсов следует вставить соответствующие операторы. Важно при этом проверить эрмитовость полученного оператора.

Так классическая формула для кинетической энергии 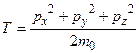, где 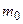- масса частицы, позволяет записать оператор кинетической энергии в виде:

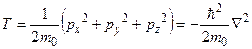. (6.24)

Легко видеть, что если 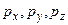- эрмитовые операторы, то и квадраты их, а затем и сумма последних есть эрмитов оператор.

По классической формуле для механического момента импульса движущейся частицы

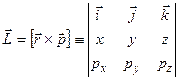
легко записать операторы проекций и квадрата механического момента:

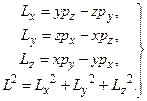(6.25)

Не составляет труда проверить линейность и эрмитовость этих операторов.

В теоретической физике большое значение имеет функция Гамильтона: 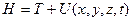. Оператор ее называется гамильтонианом квантовой системы. Если учесть, что время 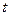в квантовой механике считается параметром, то гамильтониан частицы, движущейся в переменном потенциальном поле, имеет вид:

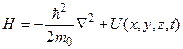. (6.26)

В случае стационарных потенциальных полей, когда 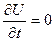, функция Гамильтона 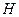, равная сумме кинетической и потенциальной энергии, представляет полную энергию 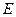, поэтому гамильтониан в этом случае является оператором энергии:

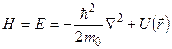. (6.27)

Уравнение для собственных функций и собственных значений оператора 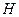в этом случае называется стационарным уравнением Шредингера или уравнением для стационарных состояний

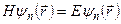. (6.28)

Date: 2015-05-18; view: 554; Нарушение авторских прав