Правила квантования

Дла квантовомеханической системы результата измерения физической величины А, изображающейся эрмитовым оператором Â, в общем случае неоднозначен. Квантовая механика, как статистическая теория, должна предсказывать не только значения результатов измерения физической величины А, но и вероятности w_n возможных значений а_n этой величины в состоянии системы, которое описывается y вектором гильбертова пространства. Эти вероятности w_n и определяются пятым постулатом. Согласно четвертому: φ₁ 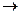а₁; φ₂ 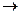а₂, т.к. φ₁ и φ₂ – возможные состояния, тогда согласно третьему: Ψ = с₁φ₁ + с₂φ₂ – возможное состояние системы и вероятности w₁ = | с₁ | 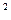и w₂ = | с₂ | .

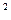Пятый постулат – правила квантования – гласит: для системы, находящейся в состоянии Ψ, вероятность W_к получить при измерении физической величины А значение а_n равна квадрату модуля соответствующего коэффициента Фурье – разложения вектора Ψ по собственным векторам φ_n оператора Â, изображающего эту физическую величину:

W_n = | (φ_n, Ψ) | 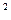= | c_n | 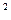(5.5)

При непрерывном спектре собственных значений оператора Â квадрат модуля коэффициента Фурье–разложения | (φ_а, Ψ) | 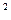следует рассматривать как плотность вероятности.

В качестве примера рассмотрим результаты измерения величины А в состоянии квантовомеханической системы, когда Ψ = φ₁, где φ₁ – собственный вектор оператора Â, определяемый уравнением Âφ_n = а_nφ_n. В этом случае вероятность W₁ измерения значения а₁ равна 1, т.к. с₁ = (φ₁, φ₁) = 1, все же другие коэффициенты в разложении Ψ= с₁φ₁ + …с_nφ_n +…= 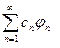равны нулю: (φ_n, φ₁) = 0 при n ≠ 1 в силу ортогональности собственных векторов эрмитовых операторов. Значит, полученные результаты можно записать в виде:

W_n =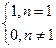

Если же вектор состояния Ψ системы не совпадает ни с одним из собственных векторов φ_n оператора Â, то используя разложение Ψ в ряд Фурье по полной системе ортонормированных собственных векторов φ_n (4.42) и вычисляя коэффициенты с_n разложения по формуле (4.43), на основе четвертого постулата запишем:

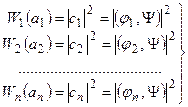, (5.7)

Очевидно, что

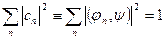(5.8)

что легко доказать, учитывая, что норма вектора Y равна единице:

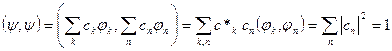
Из рассмотренных примеров следует, что пятый постулат, определяющий вероятности W_n измерения тех или иных дозволенных значений физической величины, вполне логично назвать правилами квантования.

Date: 2015-05-18; view: 588; Нарушение авторских прав