Векторы состояния в координатном представлении

Рассмотрим ради простоты одномерный случай: частица движется вдоль оси Ox.

Собственные векторы эрмитова оператора координаты являются базисными в координатном представлении. Обозначив их через 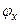, запишем уравнение для собственных векторов и собственных значений оператора :

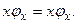(6.1)

Аналогично, собственный вектор 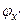, принадлежащий конкретному значению координаты , удовлетворяет уравнению:

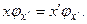(6.2)

Любой вектор Y гильбертова пространства, определяющий состояние одномерной квантовой системы, может быть разложен в интеграл Фурье по базисным векторам 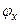согласно формуле:

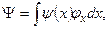(6.3)

где коэффициенты разложения записываются в виде:

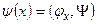(6.4)

и представляют собою координаты вектора 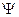или его проекции на базисные векторы 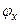в координатном представлении.

Вектор 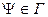обладает единичной нормой 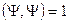, причем норму вектора Y можно представить следующим выражением:

.

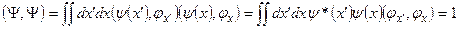Этому условию можно удовлетворить, если считать, что собственные векторы 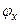оператора с непрерывным спектром собственных значений нормируются на 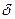-функцию Дирака:

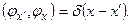(6.5)

Тогда

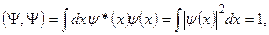(6.6)

т.е. в координатном представлении проекциями вектора Y являются значения комплексной функции 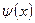при различных значениях , и что 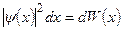- вероятность обнаружения частицы с координатой из интервала 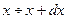. Следовательно, квадраты модулей коэффициентов Фурье-разложения (6.4) представляют известную формулу плотности вероятности .

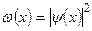Таким образом, совокупность проекций 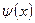или координат Y–вектора определяет этот вектор Y в координатном представлении. Другими словами, множество проекций (координат) 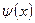называют вектором состояния в координатном представлении или коротко волновой функцией.

Формула (6.5) свидетельствует об ортогональности собственных векторов эрмитова оператора :

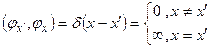, (6.7)

в то же время норма собственных векторов 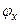равна ∞.¹

Определим скалярное произведение двух векторов y и c гильбертова пространства в координатном представлении. Записывая векторы y и c в форме разложения по базисным векторам в координатном представлении

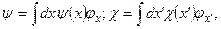
получим

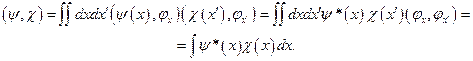(6.8)

Эта формула является обобщением выражения скалярного произведения геометрических векторов на случай векторов гильбертова пространства.

Date: 2015-05-18; view: 560; Нарушение авторских прав