Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Операторы физических величин
|
|
Ранее было сказано, что состояние квантовой частицы определяется не координатами и импульсом, а заданием Ψ- функции, вид которой зависит от конкретного потенциального поля (1-ый постулат квантовой механики). Волновая функция, описывающая сама по себе распределение по координатам, определяет также распределение по импульсам и другим динамическим характеристикам частицы, таким как кинетическая энергия, момент импульса и др.
Таким образом Ψ- функция полностью определяет не только «положение» частицы, но и все её динамические характеристики.
Для получения информации о физических величинах, связанных с движущейся частицей, в квантовой механике разработан специальный математический аппарат, в котором используют операторы физических величин и результаты их действия на волновую функцию.
Оператором называют символическое обозначение математической операции, которую необходимо совершить с интересующей нас функцией. Примером оператора могут служить умножение на х, или на какую-либо функцию f(x), дифференцирование по х т.е.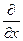 
; 
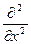, операторы набла - 
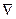, лапласиан - 
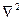и т.д.
В квантовой механике операторы принято обозначать буквами со «шляпкой», например,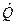 
, а его действие на некоторую функцию f(x) записывают как 
.
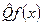Некоторые свойства операторов:
1). Операторы можно складывать: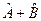 
. Действие такого суммарного оператора на любую функцию f(x) даёт результат
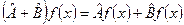
2). Под произведением операторов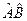 
понимают оператор, результат действия которого на любую функцию f(x) равен
.
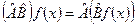Т.е. функция f(x) сначала подвергается действию оператора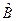 
, а затем полученный результат – действию оператора 
.
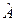Следует иметь ввиду, что не всегда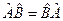 
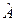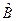. Если такое равенство соблюдается, то это значит, что операторы и коммутируют друг с другом (коммутирующие операторы).
Пример некоммутирующих операторов – это х и :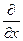
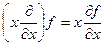, а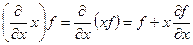 
.
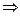
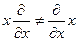3). Оператор 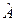называют линейным, если для любых двух функций f 1 и f 2 и любых постоянных а 1 и а 2 выполняется соотношение
.
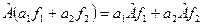С линейностью операторов связан принцип суперпозиции состояний.
Оператором физической величины может быть только линейный самосопряжённый (эрмитов) оператор. Самосопряжённым называют оператор, который совпадает со своим сопряжённым оператором. В этом случае для произвольных функци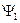й 
и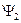 
тождественно выполняется следующее интегральное равенство
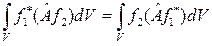
4). Если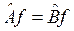 
то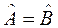 
.
Date: 2015-05-18; view: 1117; Нарушение авторских прав