Лекция 6. Квантовый гармонический осциллятор

Квантовый гармонический осциллятор

(параболическая потенциальная яма)

Гармоническим осциллятором называется система, способная совершать гармонические колебания. Примером таких колебаний в квантовой механике являются колебания атомов в твёрдых телах, молекулах и т.д.

На рисунке слева изображена потенциальная энергия U взаимодействия атомов в двухатомной молекуле (типа NaCl) в зависимости от расстояния r между ядрами атомов. Из вида кривой U (r) следует, что атомы в молекуле могут совершать колебания относительно равновесного расстояния r₀ между ядрами.

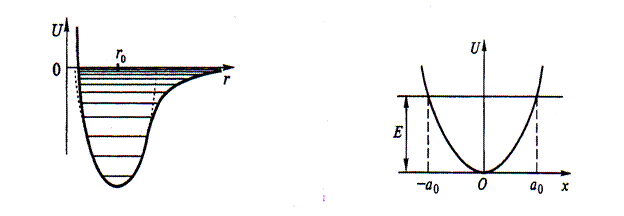
Квантово-механическая задача о гармоническом осцилляторе сводится к задаче о движении частицы вдоль оси ох в параболической потенциальной яме под действием возвращающей квазиупругой силы (рисунок справа) F_x = – kx.

Выражение для потенциальной энергии такого осциллятора имеет вид

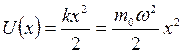, где

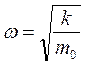- собственная частота классического гармонического осциллятора.

Графиком этой функции U (x) является парабола.

Точки х = – а₀ и х = а₀, в которых полная энергия E = U(x), являются для классической частицы точками поворота.

Амплитуду колебаний находим из выражения

.

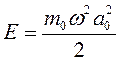
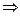
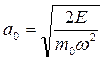Уравнение Шрёдингера в данном случае имеет вид

.

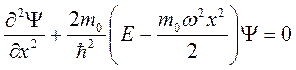Это уравнение имеет конечные, однозначные, непрерывные и гладкие решения (собственные функции) при собственных значениях Е, равных

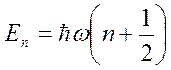, где n = 0, 1, 2, 3, …

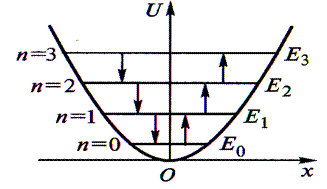
Энергетические уровни расположены на одинаковом расстоянии друг от друга .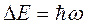

Минимальная энергия (её называют нулевой энергией)

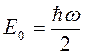
Отличие от нуля минимальной энергии осциллятора характерно для всех квантовых систем и является следствием принципа неопределённостей.

Для квантового осциллятора возможны переходы лишь между соседними «стационарными» уровнями, при которых квантовое число n изменяется на единицу ∆n = 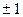(правило отбора). При каждом из этих переходов испускается или поглощается фотон с энергией 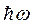, где 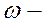его циклическая частота.

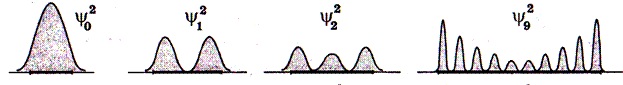
На следующем рисунке приведены графики распределения плотности вероятности Ψ ²(х) месторасположения частицы при n = 0, 1, 2, 9.

n = 0 n = 1 n = 2 n = 9

Жирными отрезками на оси ох показаны интервалы, на концах которых E = U. Классическая частица при колебаниях за пределы интервала заходить не может. Квантовая частица может быть обнаружена и вне пределов этих интервалов.

Date: 2015-05-18; view: 1083; Нарушение авторских прав