
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Соотношения неопределённостей
|
|
В классической физике исчерпывающее описание состояния частицы определяются динамическими параметрами, такими как координаты, импульс, момент импульса, энергия и др.
Отличие микрочастицы от макроскопической частицы заключается в том, что существует принципиальный предел точности, с которой подобные параметры могут быть указаны и измерены. В частности, для описания движения микрочастицы понятие траектории в некоторых случаях оказывается неприемлемым (интерференция электрона от двух щелей).
Отличие микрочастицы от электромагнитной волны состоит в том, что свет, используя, например, полупрозрачное зеркало, можно разделить на две части и отдельно исследовать каждую из них. Микрочастица во всех опытах проявляет себя как единое целое. Нельзя наблюдать часть электрона или нейтрона.
Пусть электроны падают нормально на непрозрачную преграду, в которой имеется щель АВ шириной ∆х
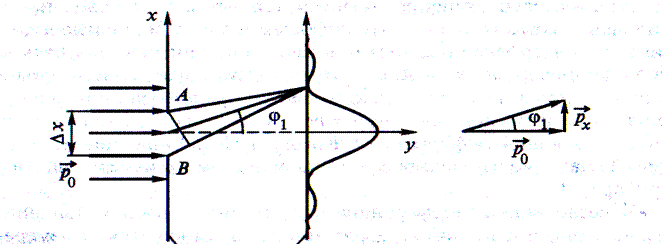
Если падающие электроны обладают определённым импульсом р0, то этим электронам соответствует плоская волна с 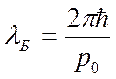 и волновым вектором
и волновым вектором 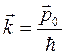
Поскольку волна распределена по всему пространству, то каждый электрон до прохождения через щель имеет точно определённый импульс 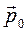 (px= 0, py= p0, pz= 0) и неопределённую координату х.
(px= 0, py= p0, pz= 0) и неопределённую координату х.
При прохождении электрона через щель ситуация существенным образом меняется. Неопределённость координаты х становится равной
ширине щели ∆х, но при этом появляется неопределённость проекции импульса ∆ рх, обусловленная дифракцией электронов на щели.
Согласно теории дифракции 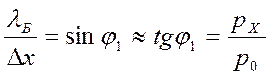
 .
.
Принимая, что ∆ рх ~ px, получаем
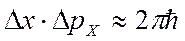 .
. 
Более строгий вывод даёт следующий результат
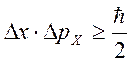
Это соотношение называется соотношением неопределённостей Гейзенберга.
Для других координатных осей:
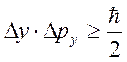 и
и 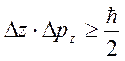 .
.
В то же время не существует никаких принципиальных ограничений на точность определения координаты и проекции импульса на другую координатную ось, например, ∆х и ∆ру.
Соотношение Гейзенберга задаёт теоретический предел точности измерения характеристик микрочастицы, но никак не связано с погрешностью измерений конкретных измерительных приборов.
На практике для оценочных расчётах часто используют соотношение
∆х.∆рх 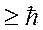
С помощью соотношения неопределённостей можно получать важные физические результаты, а также проводить численные оценки, не прибегая к точному но трудоёмкому решению задачи.
Рассмотрим для примера атом водорода и будем считать, что электрон движется вокруг ядра по круговой орбите радиуса r со скоростью v

Будем считать, что ∆х = r, a ∆p = p = mev. Тогда rmev 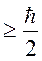 и
и
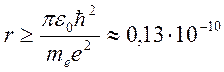 м
м
Следовательно, радиус орбиты электрона, т.е. радиус атома не может быть меньше найденного значения. В свою очередь это означает, что электрон не может упасть на ядро, т.е. атом является устойчивым образованием.
Кроме координат и проекций импульса существуют другие пары физических величин, которые не могут быть измерены одновременно точно. Особо следует выделить соотношение, которое называется соотношением неопределённостей для энергии и времени
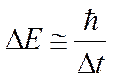
|
Система, имеющая среднее время жизни ∆t, не может быть охарактеризована определённым значением энергии. Разброс энергии 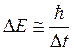 возрастает с уменьшением времени жизни системы и частота излучения также должна иметь неопределённость
возрастает с уменьшением времени жизни системы и частота излучения также должна иметь неопределённость 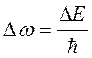 , т.е. спектральные линии должны иметь конечную ширину (уширение).
, т.е. спектральные линии должны иметь конечную ширину (уширение).
Следствия из соотношений неопределённостей:
1) Первым следствием из соотношения неопределённостей является отсутствие траектории у микрочастиц ( для частиц с высокой энергией и ∆х 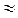 10-6 м неопределённость импульса ∆рх =
10-6 м неопределённость импульса ∆рх = 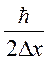 ~ 10-28 кг.м/с,что значительно меньше значения самого импульса р. Это означает, что для этих частиц λ Б оказывается очень малой и для описания поведения таких частиц должна применяться классическая механика и можно говорить о траектории частицы).
~ 10-28 кг.м/с,что значительно меньше значения самого импульса р. Это означает, что для этих частиц λ Б оказывается очень малой и для описания поведения таких частиц должна применяться классическая механика и можно говорить о траектории частицы).
2) Отсутствие состояния покоя. Если ∆х = а, то ∆рх 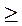
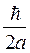 . Полагая рх мин
. Полагая рх мин 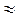 ∆рх мин находим минимальную (не равную нулю) энергию микрочастицы
∆рх мин находим минимальную (не равную нулю) энергию микрочастицы
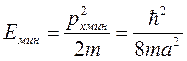 ,
,
т.е. в квантовой механике микрочастица не может находится в состоянии полного покоя.
3) Теряет смысл деление полной энергии частицы на кинетическую и потенциальную. Кинетическая энергия зависит от импульса частицы, а потенциальная энергия от её координаты. Но координата и импульс не могут одновременно иметь определённые значения. Равенство Е = К + U для мгновенных значений невозможно (в квантовой механике принято потенциальную энергию обозначать буквой U). Такое равенство справедливо лишь для средних значений энергии
<E> = <K> + <U>.
Date: 2015-05-18; view: 1143; Нарушение авторских прав