Статистический смысл волновой пси-функции

Для микрочастиц из-за соотношения неопределённостей теряет смысл классическое определение состояния частицы (координаты и импульса).

В соответствии с корпускулярно-волновым дуализмом в квантовой теории состояние частицы задаётся пси-функцией Ψ (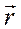, t), которая является комплексной величиной и формально обладает волновыми свойствами.

Движение любой микрочастицы по отдельности подчиняется вероятностным законам. Распределение вероятности, характеризующее это движение, проявляется в регистрации достаточно большого числа частиц. Это распределение оказывается таким же, как распределение интенсивности волны: там, где интенсивность волны больше, регистрируется и большее число частиц.

В квантовой теории постановка вопроса состоит не в точном предсказании событий, а в определении вероятностей этих событий, по которым по определённым правилам рассчитывают средние значения физических величин.

Пси-функция Ψ (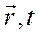) и является той величиной, которая позволяет находить эти вероятности.

Квантовая механика базируется на нескольких постулатах. Правильность этих постулатов может быть подтверждена сравнением предсказаний квантовой механики с результатами экспериментов.

Первый постулат квантовой механики гласит: состояние частицы вквантовой механике описываетсяволновой функцией Ψ ( 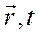), являющейся функцией пространственных координат и времени и имеющей вероятностный смысл т.е. определяющей вероятность нахождения частицы в различных областях пространства.

Волновая функция Ψ ( 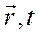) в нерелятивистском случае находится из уравнения Шрёдингера.

Остальные постулаты будут приведены позже.

Если w = 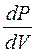- плотность вероятности того, что в момент времени 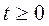частица может быть обнаружена в точке пространства М = М(х,y,z) то

w = Ψ^.Ψ* = 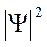, где

Ψ* - функция, комплексно сопряжённая с функцией Ψ, являющейся в общем случае комплекснозначной функцией.

Вероятность того, что частица будет обнаружена в любой области пространства конечного объёма V можно рассчитать

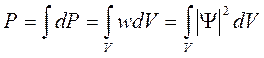
Так как вероятность нахождения частицы во всём пространстве 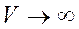равна единице, то

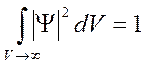
Иногда интеграл берётся не по всему пространству, а по той области, в которой Ψ-функция отлична от нуля.

Данное соотношение называют условием нормировки волновой функции, которое означает, что во всей области, где 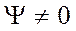, частица находится с достоверностью.

На волновую Ψ- функцию накладываются определённые ограничения – так называемые условия регулярности волновой функции:

волновая функция должна быть конечной, однозначной и непрерывной функцией пространственных координат, за исключением, быть может отдельных точек. Непрерывными должны быть также частные производные

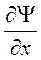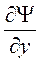; и .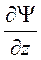

Принцип суперпозиции квантовых состояний: если частица может находится в квантовом состоянии Ψ ₁, а также в другом квантовом состоянии Ψ ₂, то эта частица может также находится в квантовом состоянии, описываемом волновой функцией

Ψ = С₁Ψ₁ + С₂Ψ₂, где

С₁ и С₂ - в общем случае комплексные числа.

Для нормированных функций

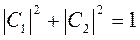
Date: 2015-05-18; view: 1058; Нарушение авторских прав