Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать неотразимый комплимент
Как противостоять манипуляциям мужчин?
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Одномерный потенциальный порог и барьер
|
|
Движение частицы в области потенциального порога
Потенциальным порогом ( потенциальной стенкой ) называют силовое поле, в котором потенциальная энергия частицы имеет вид
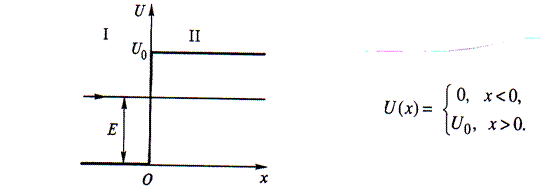
Пусть слева на порог налетает частица с полной энергией Е . На языке квантовой теории это означает, что на порог слева «падает» дебройлевская волна
.
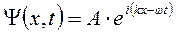Чтобы удовлетворить граничным условиям для Ψ и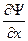 
при х = 0, должны существовать как прошедшая волна, так и отражённая. Так как ω в этих волнах одна и та же 
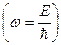, то в расчётах можно ограничиться только координатной частью этих волн, а именно Ψ( х ).
Задача состоит в том, чтобы сначала найти амплитуды отражённой и падающей волн, а затем коэффициенты отражения R и пропускания D .
Уравнение Шрёдингера для частицы в данном силовом поле имеет вид:
в области I( x < 0 )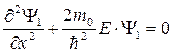 
в области II( x > 0 )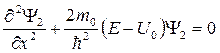 
1).Низкий порог ( Е > U0 )
Общее решение уравнения Шрёдингера имеет вид:
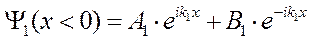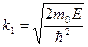
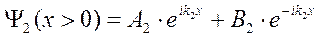, где 
, где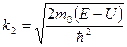 
Будем считать, что падающая волна характеризуется амплитудой А1 , причём вещественной, а отражённая – амплитудой В1 . В области II( x > 0) имеется только проходящая волна, поэтому В2 = 0 .
Из условия непрерывности Ψ и 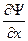в точке х = 0 следует, что 
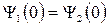или 
и
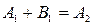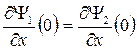или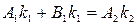 
Тогда
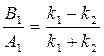и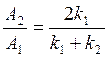 
Для определения коэффициентов R и D вводят понятие плотности потока вероятности j , вектор которого определяется через волновую функцию следующим образом:
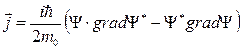
В соответствии с видом Ψ-функции для падающей, отражённой и прошедшей волн имеем:
jпад ~ k1A12 , jотр ~ k1B12 и jпрош ~ k2A22
Теперь можно записать
для коэффициента отражения
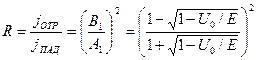
для коэффициента пропускания
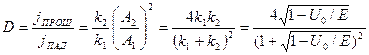
Видно, что R + D = 1 , что и должно быть по определению. Коэффициенты R и D не зависят от направления движения частицы: слева направо или наоборот.
В классическом случае при E > U0 должно быть R = 0.
Эффектнадбарьерного отражения( R > O ) является чисто квантовым и объясняется наличием у частицы волновых свойств.
2). Высокий порог ( E < U0 ).
В этом случае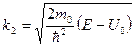 
является чисто мнимым. Коэффициент отражения 
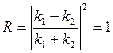т.к. числитель и знаменатель –
величины комплексно-сопряжённые. Таким образом, отражение будет полным, а D = 0.
Но волновая функция при x > 0 не обращается в нуль, т.е. микрочастицы могут проникать в области, которые для макроскопических частиц недоступны.
Плотность вероятности нахождения частицы в области II определяется выражением
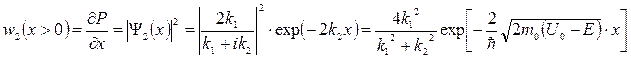и зависит от массы т0 , разности ( U0 – E ) и расстояния от границы порога.
Для электрона с (U0 – E) = 1 эВ вероятность нахождения на расстоянии от порога сравнимым с размерами атома ( х = 10-10 м ) достаточно велика, а на расстоянии в 10 раз большем ( х = 10-9 м ) ничтожно мала.
Отражение хотя и является полным (R = 1) не обязательно происходит на самом пороге. Частица может проникнуть в область II , а затем выйти из неё ( аналогично полному внутреннему отражению в оптике).
Прохождение частицы через потенциальный барьер.
Рассмотрим одномерный прямоугольный потенциальный барьер
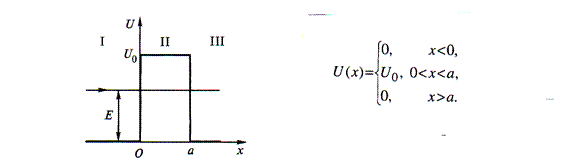
Частица движется слева направо. Слева от барьера имеем падающую и отраженную волну, а за барьером только прошедшую волну.
Уравнение Шрёдингера для областей I, II и III имеет вид:
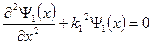
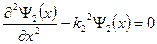
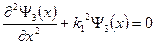
Где
, 
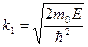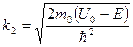
Волновые функции, являющиеся решением этих уравнений
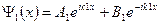
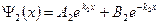
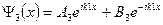
Из решения этой системы уравнений получают, применив некоторые упрощающие допущения, выражение для коэффициента прозрачности D прямоугольного барьера
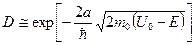
Для потенциального барьера произвольной формы
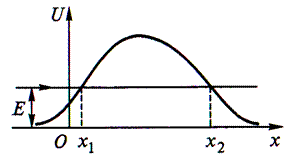
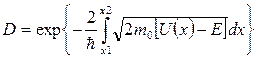
Пределы интегрирования х1 и х2 определяют из решения уравнения U( x ) = E .
Туннельный эффект
Прохождение частицы через потенциальный барьер, высота которого превышает энергию частицы, получило название туннельного эффекта (частица, проходя под барьером, как бы движется в туннеле). При прохождении через барьер полная энергия частицы Е не меняется.
Туннельный эффект представляет собой чисто квантовое явление.
Этим эффектом объясняются многие физические явления; например, холодная эмиссия электронов из металла (автоэмиссия), альфа-распад, спонтанное деление ядер и др.
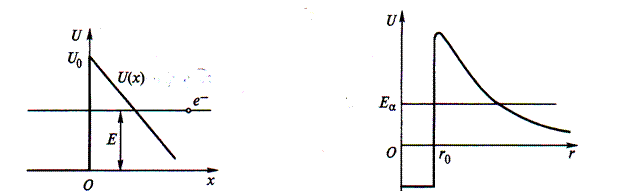
На левом рисунке представлен потенциальный барьер треугольной формы, имеющий место на границе металл-вакуум в явлении холодной эмиссии электронов из металла. Электрон в металле находится в потенциальной яме глубиной U0 . Если вблизи поверхности металла имеется электрическое поле напряжённостью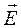 
, способствующее выходу электронов из металла, то потенциальная энергия электрона вблизи поверхности металла может быть представлена в виде
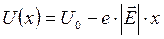
При туннелировании электронов через этот барьер происходит их выход из металла даже при низких температурах.
На правом рисунке представлен потенциальный барьер α-частицы в поле ядра. На больших расстояниях r между α-частицей и ядром действуют силы кулоновского отталкивания и потенциальная энергия частицы
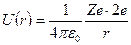, где
Ze – заряд дочернего ядра; 2е – заряд α-частицы.
Внутри ядра (r < r0 ) α-частица находится в потенциальной яме, выйти из которой она может только за счёт туннельного эффекта.
Прохождение частицы над барьером ( E > U0 )
Частица массой т0 падает на прямоугольный потенциальный барьер высотой U0 и шириной а . Энергия частицы Е больше высоты барьера.
В этом случае решение системы уравнений Шрёдингера для трёх областей: I – ( x < 0 ), II – ( 0 < x < a ), III – ( x > a )даёт следующие значения для коэффициента прохождения D .
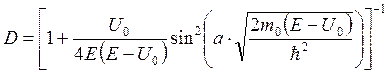
Частица беспрепятственно проходит над таким барьером ( D = 1) при значениях энергии равных
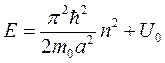, где n = 1, 2, 3, … ( sin = 0 )
При других значениях энергии существует отличная от нуля вероятность отражения частицы от барьера.
Пролёт частицы над потенциальной ямойконечной глубины ( E > U0 )
Частица пролетает над потенциальной ямой конечной глубины U0 и ширины а слева направо вдоль оси ох.
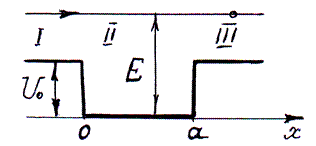
Решая систему уравнений Шрёдингера для трёх областей, получаем выражение для коэффициента прохождения D , характеризующего вероятность прохождения частицы над ямой:
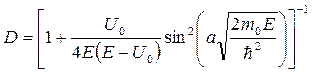
Коэффициент прохождения D зависит от соотношения между энергией частицы и глубиной потенциальной ямы и в общем случае оказывается меньше единицы (частица может отразится от потенциальной ямы даже если E > U0 ). Данное явление, полностью отсутствующее в классической физике, объясняется наличием у частицы волновых свойств.
Частица не испытывает отражения на границах ямы ( D = 1 ) только если sin = 0 . Это условие выполняется при значениях энергии частицы
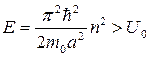, где n = 1, 2, 3, …
Рассмотренная модель поведения частицы вблизи симметричной прямоугольной потенциальной ямы конечной глубины хорошо качественно описывает движение электрона вблизи атома. В частности, проведённый анализ даёт квантово-механическое объяснение эффекта Рамзауэра, где наблюдалась аномальная прозрачность атомов инертных газов для пучка электронов при определённых значениях кинетической энергии (K = E – U0).
Условие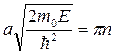 
можно представить в виде 
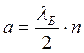(λБ – длина волны де Бройля электрона внутри ямы ). Это условие определяет гашение за счёт интерференции волн, отражённых от двух границ ямы аналогично просветлению оптики при интерференции двух электромагнитных волн от двух сторон просветляющей тонкой плёнки.
Date: 2015-05-18; view: 4696; Нарушение авторских прав