Частица в потенциальной яме с непроницаемыми стенками

КВАНТОВАЯ 2

Лекция 5

Стационарные задачи квантовой механики

Итак – уравнение Шрёдингера для стационарных состояний

,

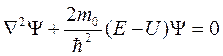а волновая функция частицы, находящейся в стационарном квантовом состоянии, имеет вид

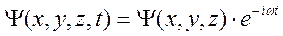, где .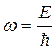

Плотность вероятности обнаружения частицы при этом

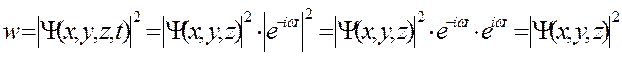
т.е. не зависит от времени.

В стационарных состояниях от времени также не зависят вектор плотности потока вероятности 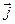и средние значения физических величин.

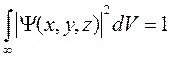
Частица в потенциальной яме с непроницаемыми стенками.

Одномерная потенциальная яма

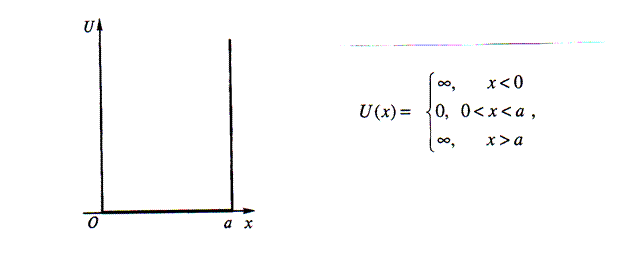
Потенциальная энергия частицы внутри ямы (0 < x < a) постоянна и равна нулю, а вне ямы обращается в бесконечность.

Уравнение Шредингера для одномерного движения частицы вдоль оси ОХ:

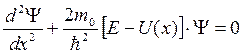
Так как вне ямы 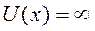, то для выполнения этого условия необходимо, чтобы 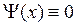. В силу непрерывности функция Ψ(х) должна обращаться в нуль и на границах ямы.

Таким образом, задача о движении частицы в одномерной прямоугольной потенциальной яме с непроницаемыми стенками сводится к решению уравнения

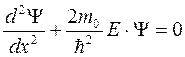при 0 < x < a

с граничными условиями Ψ(0) = 0 и Ψ(а) = 0.

Введя обозначение 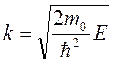получаем 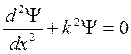. Из теории колебаний известно, что решением этого уравнения является выражение

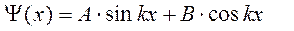или .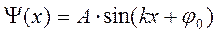

Используя граничное условие Ψ (0) = 0 получаем В = 0 ( ил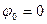и )и

.

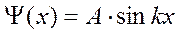Используя граничное условие Ψ(а) = 0 получаем

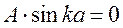и если 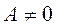. то 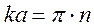, где n = 1; 2; 3 …

Значение n = 0 не удовлетворяет условию задачи т.к. при этом 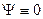, а это означает, что частица в яме отсутствует.

Таким образом 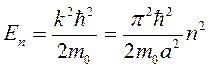, где n = 1; 2; 3 …

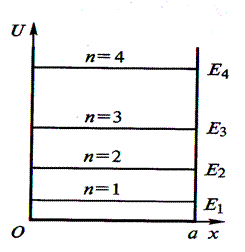
Видно, что частица, находящаяся

в потенциальной яме, может иметь

только дискретные, квантовые значения

Date: 2015-05-18; view: 1192; Нарушение авторских прав