Энергии

Число n называют квантовым

числом, а соответствующее ему значение

Е_n – уровнем энергии. Уровень Е ₁

называется основным состоянием, а все

остальные – возбуждёнными (n = 2 -

- первое возбуждённое состояние).

Энергетическое расстояние между соседними уровнями

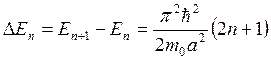
Для молекулы газа с т ₀ ~ 10^{-27 кг} в сосуде размером а = 0,1 м и n > 1 получаем

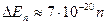эВ,

т.е. 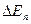намного меньше энергии теплового хаотического движения молекулы ( 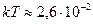эВ) и дискретностью энергетического спектра движущейся молекулы можно пренебречь.

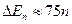Для свободного электрона в атоме ( м) получаем эВ и это сравнимо сэнергией связи электрона в атоме Е _СВ ~ 10 эВ.

Волновая функция частицы в одномерной прямоугольной потенциальной яме

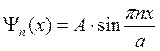
Множитель А находим из условия нормировки Ψ- функции:

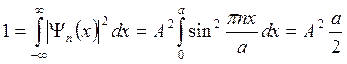
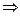
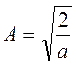и тогда окончательно

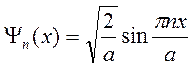при (0 < x < a).

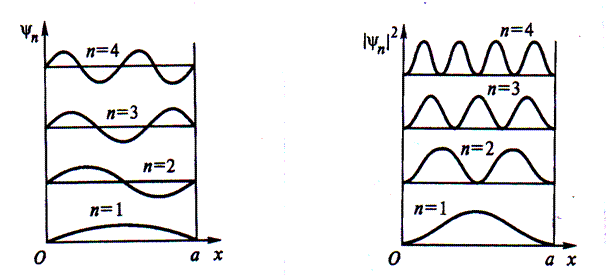
В основном состоянии частица с наибольшей вероятностью находится в середине ямы, а в 1-ом возбуждённом состоянии (n = 2) вероятность нахождения частицы в центре ямы равна нулю, хотя пребывание частицы в левой и правой половинах ямы равновероятно.

Плотность вероятности нахождения частицы в основном состоянии:

,

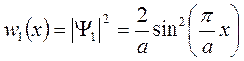в первом возбуждённом состоянии:

.

Вероятность нахождения частицы в области x ₁ < x < x ₂ , где x ₂ < a

в основном состоянии:

,

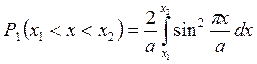в первом возбуждённом состоянии:

.

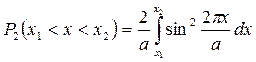Двумерная потенциальная яма

Рассмотрим частицу, находящуюся в двумерной прямоугольной потенциальной яме с бесконечно высокими стенками.

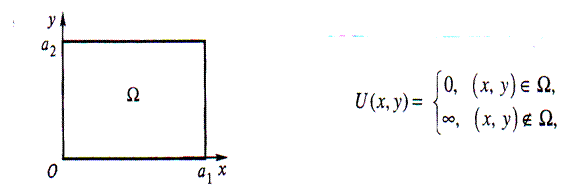
Где Ώ = 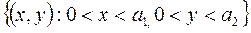-прямоугольная область на плоскости (х,у).

Вне потенциальной ямы .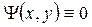

Поскольку движение частицы в яме вдоль осей ох и оу происходит независимо, то

,

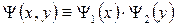а уравнение Шрёдингера имеет вид

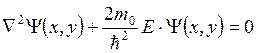или

Разделив левую и правую часть на 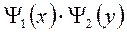получаем

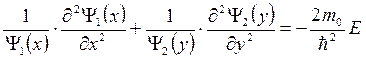
Поскольку в правой части уравнения стоит постоянная величина, то и слева оба слагаемых должны быть постоянными величинами, и представив энергию Е в виде двух слагаемых Е = Е ₁ + Е ₂ можно разделить уравнение Шрёдингера для двумерной задачи на два одномерных уравнения:

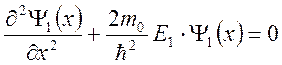и ,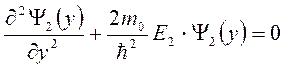

решения которых такие же как и для одномерного случая:

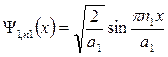и 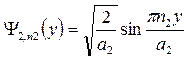, где n ₁; n ₂ = 1, 2, 3, …

В результате нормированная волновая функция частицы, находящейся в двумерной прямоугольной потенциальной яме с бесконечно высокими стенками:

. а энергия .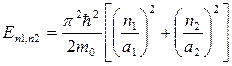

Если потенциальная яма квадратная (а ₁ = а ₂ = а) то

, где n ₁; n ₂ = 1, 2, 3, …

Видно, что одному и тому же энергетическому уровню Е_n1,n2, определяемому квантовыми числами n ₁ и n ₂ при n ₁ 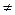n ₂ соответствуют два различных состояния частицы, описываемых волновыми функциями Ψ_n1,n2 и Ψ_n2,n1.

Энергетический уровень, которому соответствует несколько состояний частицы называется вырожденным энергетическим уровнем.

Энергетический уровень, которому соответствует только одно состояние частицы, называется невырожденным. Для квадратной потенциальной ямы невырожденными являются энергетические уровни, для которых n ₁ = n ₂.

Трёхмерная потенциальная яма (потенциальный ящик)

Здесь G = 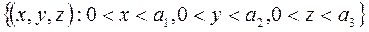- внутренняя область прямоугольного параллелепипеда.

Вне ящика , а внутри .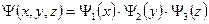

Используя тот же метод, что и для двумерной ямы получаем

 

; ;

 

 

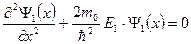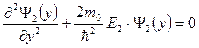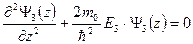
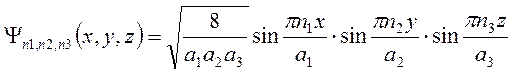
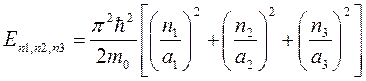, где

 

n ₁, n ₂, n ₃ = 1, 2, 3, … - квантовые числа.

 

В кубическом потенциальном ящике (а ₁ = а ₂ = а ₃ = а) получаем

 

.

Энергетические уровни в кубической потенциальной яме, для которых n ₁ = n ₂ = n ₃, являются невырожденными, все остальные уровни вырождены.

 

Число вырожденных состояний определённого энергетического уровня называется кратностью вырождения уровня. Вопрос о кратности вырождения энергетических уровней в кубической яме рассматривается в задаче на семинарском занятии.

 

Плотность вероятности нахождения частицы в единице объёма для основного состояния в кубической яме:

 

.

 

Вероятность нахождения частицы в основном состоянии в некоторой области 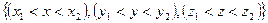, где x ₂, y ₂, z ₂ < a

 

.

 

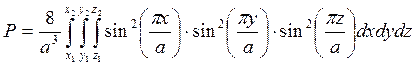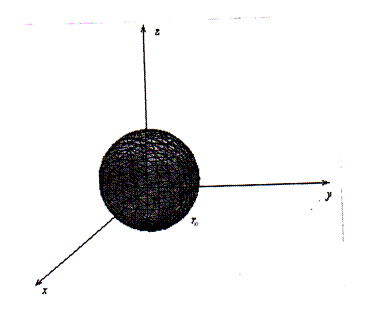
Cферически-симметричная потенциальная яма радиусом а

 

U (r) = 0 при r < a и U (r) = 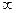при r > a.

Уравнение Шрёдингера для области r < a:

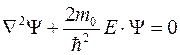
В сферически-симметричной яме Ψ -функция не зависит от угловых координат θ и φ и можно использовать только радиальную составляющую оператора Лапласа

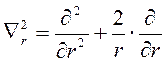, т.е.

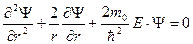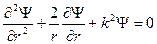или , где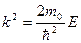

 

Для решения этого уравнения используют подстановку 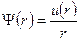. Тогда

 

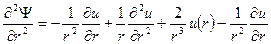
После подстановки получаем

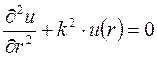
Решение этого уравнения имеет вид

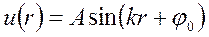
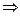
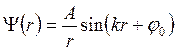
Так как Ψ(r) 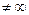при r = 0 то получаем φ ₀ = 0.

 

Используя условие непрерывности Ψ –функции, имеем

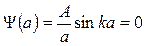
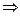
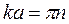, где n = 1, 2, 3, …

(c учётом того, что ).

 

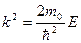Коэффициент А находим из условия нормировки:

 

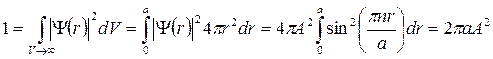
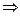
Таким образом

.

 

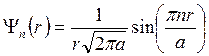Плотность вероятности (вероятность нахождения частицы в шаровом слое единичной толщины) в основном состоянии:

 

.

 

⇐ Предыдущая11121314151617181920Следующая ⇒

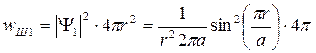
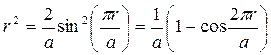Date: 2015-05-18; view: 908; Нарушение авторских прав

Понравилась страница? Лайкни для друзей: