
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Х—? у~~? г — ? а)(3;2;6); Ь)(3; -2; 6); 4; б); й;г(|;4;6); е)&Л
|
|
Ъ) 2;
С)-и
й) -2; е)0.
4.
С(4;0;4), созф
| »>-й; |
| , 13 с>> ю; |
| й> /о; |
5. АВСВ — трапеция, ЕР средняя линия. АВ • ЕР —? а) 10;
с) 7;
6.
ОАВС — параллелограмм. у = АВЕС. ф—? а; 90°;
&/45°; с; -45°;
й; зо°;
е; 60°.
АВСО — трапеция, ЕР — общая средняя линия для трапеции и треугольника.
ВС(2;1;-2),
~МК{х;у;г)-1 а;(-3;-^;3); ь;(-7;^^;
сД7; ^;-7); й;(^;7;-7);
8. |АВ| = |АС| = \АЦ = 6 см, \ВС\ = 4 см, |Б^1 = 2 см,
22; Ь) 24; с; 27; й; 30; е,) 32.
9. |АО| = 10см,
АВС1) — квадрат, ос±р. о; 10; &;12; с) 13;
10. а ± Р, |АО| = |ВС| = 3 см, \ВЦ = \АС\ = 4 см,
А(2,3,0)
| 237 238. 239 |
 Ф=АД ВС.
Ф=АД ВС.
СО8 ф —?
7 ,,7
Е>1
Дополнительные задачи
232. АВСВ — параллелограмм, а точка Е на стороне ВС такая, что
\ВЕ\: \ЕС\ = 2:3. Выразите вектор АЕ через векторы АВ и АС •
233. Докажите, что если диагонали четырехугольника при пересечении
делятся пополам, то такой четырехугольник есть параллелограмм.
234. Докажите, что отрезок, соединяющий середины диагоналей
трапеции, параллелен основаниям.
235. Дан параллелепипед АВСВА1В1С1В1. М,М,Р — середины отрез
ков ВВг, СВХ, ВСг соответственно. Разложите по векторам
р = АВ~1, д = АО, г = ААх векторы: 1) АВ; 2) ~АС[; 3) АЛГ ;
4)1$, Яе[В1С1], где Щ: В~Д = 5:11.
236. Вне плоскости параллелограмма АВСВ взята точка О. Разложите по векторам а = ОА, Ь = ОВ, с=ОС векторы: 1) ОМ, где М = (АС) о (ВВ); 2)ОВ;3)ОК, где К— середина АВ. Найдите координаты вершины и координаты точки пересечения диагоналей параллелограмма АВСВ: 1) А(0; 0; 0), В(1; 2; 3), С(-1; 1; -2); 2) А(-1; 2; 1), В(0; 4; 4), С(-2; 3; -1). С помощью векторов докажите, что если прямая перпендикулярна двум сторонам треугольника, то она перпендикулярна и третьей стороне.
Три ребра тетраэдра, исходящие из одной вершины, равны, углы между ними тоже равны. Докажите, что каждое ребро такого тетраэдра перпендикулярно противоположному.
| Рис. 69 |
240. Точка К — середина ребра АС правильного
тетраэдра АВСВ. Найдите косинус угла меж
ду прямыми АВ и КВ.
241. Скорость течения реки — 1,2 м/с. Катер
движется со скоростью 3 м/с перпендикулярно
берегу. Определите скорость движения катера
по отношению к реке.
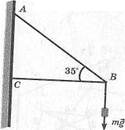
242. К концу кронштейна приложена сила
Р = т§ ~ 42 Н. Найдите силу сжатия стержня
ВС и силу растяжения стержня АВ (рис. 69).
|
| Рис. 70 |
| А |
| Рис. 71 |
243.  Проволока закреплена в точках Л и С, а в
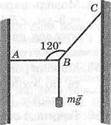
Проволока закреплена в точках Л и С, а в
точке В приложена сила Р= т§= 45 Н. Най
дите силу натяжения на участках АВ и ВС
(учитывая, что АВ расположена горизон
тально, рис. 70).
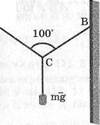
244. Проволока закреплена в точках А и В, а в
точке С приложена сила Р = тп§ = 45 Н.
Найдите силу натяжения на участках АС и
ВС, если точки А ж В находятся на одном
уровне (рис. 71).
245. Основание АВ равнобедренного треугольни
ка АВС лежит в плоскости ос (а Ф (АВС)).
Какой угол больше: 1) угол между прямой
АС и а? 2) между прямой СВ и а? (В —
середина стороны АВ).
246. Проекция равностороннего треугольника
на плоскости, проходящей через одну из его
сторон — прямоугольный треугольник. Най
дите угол между стороной треугольника и
плоскостью проекции.
247. Дан ромб с диагоналями йг и йг Через его
сторону проведена плоскость у, образующая с другой стороной угол. Найдите площадь проекции ромба на плоскость.
248. Концы отрезков АВ и СВ принадлежат параллельным плоскос
тям а и (3. Проекции этих отрезков на одну из плоскостей
соответственно равны а и Ъ, а углы ((АВ) /. а) и ((СО) А а) относят
ся как 1: 2. Найдите расстояние между плоскостями.
249. Из точек А и В, принадлежащих одной из граней двугранного угла,
проведены перпендикуляры ААг, ВВг на плоскость другой грани
и перпендикуляры АЛ„ ВВ2 на ребро. Найдите:
1) \ВВ2\, если |АА1| =15 см, \ЙВг\ = 27 см, \АА2\ = 20 см; 2) \ААХ\ и [ВБу, если \АгА0\ = тп, |ВД| = п, |АА1| + \ВВг\ = р.
250. Угол между плоскостями АВС и ВВС равен 45°. Найдите \АВ\,
если |АВ|=15 см,|ВС|=14 см, |АС|=13 см, \ВВ\=\ВС\= 9 см.
''М.Концы отрезка АВ принадлежат граням двугранного угла, равного ср. Из точек АшВ проведены перпендикуляры АС и ВВ к ребру двугранного угла. Известно, что |АС| = 10 см, \ВВ\ = 5 см, \СВ\ = 12 см. Найдите |АВ|, если: 1) <р = 90°; 2) ср = 60°.
252. Гипотенуза прямоугольного треугольника лежит в плоскости а, его катеты наклонены к этой плоскости под углами 30° и 45°. Найдите угол между плоскостью треугольника и плоскостью а.
'МУЛ. В тетраэдре АВСВ все ребра, кроме ребра ВС, имеют разные длины, АСАВ = 90°. Найдите величину двугранного угла АВ.
254. Модель параллелограмма АВСВ, у которого \АВ\ = 2 дм, \АЦ =
= 3 дм, /.ВАВ = 60°, перегнута по диагонали АС так, что обра
зовался двугранный угол в 120°. Какую величину после этого
имеет угол между сторонами АВ и АО?
255. Модель ромба со стороной а и диагональю ВВ, равной й, перегну
та по этой диагонали так, что образовался двугранный угол,
равный ф. \АС\ —?
256. Точки А и В принадлежат различным граням прямого дву
гранного угла и находятся на равных расстояниях \АА1\ и |ЛВ1| от
его ребра. Известно, что \АВ\: \АА1\ = 2. Найдите: 1) угол между
прямой АВ и ребром двугранного угла; 2) углы между прямой
АВ и каждой из его граней.
■
Ответы и указания
16. Так как С б (АВВ) и М е (АВВ), то (СВМ) = (АВВ). 18. Боли обозначим ЛГ = а п Ь, то (МЫ) — искомая прямая. 19. 1) правильно, 2) нет. (Возможно А е т). 20. 1) прямая, луч, пустое множество; 2) луч, отрезок, точка, пустое множество; 3) плоскость, полуплоскость, пустое множество; 4) полуплоскость, полоса, угол, прямая, пустое множество; б) отрезок, точка, пустое множество; 6) треугольник, четырехугольник, отрезок, точка, пустое множество. 36. Нет. 43. Если точка не принадлежит прямой, то можно провести бесконечно много плоскостей. 62. Нет. 63. Возможно; нет. 64. Нет. 67. Возможны треугольник, правильный треугольник, прямоугольный четырехугольник, квадрат, трапеция. 77. 1) 7 м; 2) \ВВ^ = а+ с + Ь. 79. Возможно, пересекутся или параллельны. 80. Пересекаются (или скрещиваются). 87. 45°. 88. 90°. 89. Бесконечно много. 90. Бесконечно много. 92. 5 см. 93. 10 см, 2743 см. 95. Возможно. 96. а) =21 см; б) зУ2а; в) «14 дм. 97. Существует. 98. 2У2 см. 99. Нет. 100. Единственная прямая; бесконечно много. 101. С плоскостью а не пересекается. 102. 9 см2. 106. 1б72см2. 107. 1) 26 см; ЗУэТсм2; 2) а (1+2 Л), ~а\
108. 1 см или 0,6 см. 109. 1) 3 см; 2) 10 дм; 3) 15 см. 111. -Д см, 4 см, =3,4 см. 113. 2 дм;
16 дм. 114. Окружность с радиусом 0,6 дм и с центром в основании перпендикуляра. 115. 1) 15 см, 41 см; 2) 15 см, 41 см. 116. 9 см; 0 см или 15 см; 9 см. 119. 12 см. 120. 5 см, 3 см. 121. Указание: а) если предположим В е а и а > Ь, то х = Ь; б)если
| 2+ аа(3-2У 2) |
 предположим А е а и а < Ь,то х = — %ц —. 122. 8 см, 17 см. 123. 4т2 + с2 • сов2а. 124. 96 см, =69,3 см. 125. 3 см. 126. 1 см. Указание: рассмотрите уравнение
предположим А е а и а < Ь,то х = — %ц —. 122. 8 см, 17 см. 123. 4т2 + с2 • сов2а. 124. 96 см, =69,3 см. 125. 3 см. 126. 1 см. Указание: рассмотрите уравнение
4 - х2 ~ 13 - 4Х2, где х — высота треугольника. 127. д/^2~-!г и
128. у1п2-Н.2. 129. 5 см. 130. 1) 4 см; 2) 3,6. 132. 35 дм. 133. 6 дм; 134. 8 м. 135. 0,5 дм;
л/2
136. '12т2-п2; *1пг-т2; 137. 2 дм. 138. 1,2 дм; 6,2 дм. 139. ~ а. 140. 2 дм.
141. Возможно, бесконечно много. 142. 1) 12 -Уз см; 12 см; 2) 16 см, 8 Уз см; 3) 10 Уз, б УЗ. 143. 50\ 144. 45*. 145. ЗУ2 дм. 146. 12У§ см. 147. бУ1см. 148. Воспользуйтесь теоремой косинусов. 149. =44 м. 151. 1) 4Убсм; 2) 2У15 см. 152. а или а-УЗ. 153. «42 см. 154.16 см. 155. ЗУЗ дм и 3 дм. 157.17 см. 160. т[а?~+ Ь2 + с2 - 2Ьс ■ совф.
■
161. 30°. 164. 13 см. 165. 30°. 166. А-У2. 167. 45°. 168. 1) Уа2+Ь2+с2"; 2) Уа2+62-с2. 169. 17 см. 170. 1)тУ2; 2)тУЗ; 3) 60°. 174. [(2; 0; 0), (0; 4; 0), (0; 0; 6), (2; 4; 0),
(0; 4; 6)]. 175. 4У2; У41. 176. Расстояние до плоскости ху равно 3, до плоскости хг равно 2, до плоскости уг равно 2; расстояния до координатных осей х,у,г соответ-
ИВенно равны У13, У13, 2У2; расстояние от начала координат У17. 177. Точка А
1 1 ближе. 178. (-1, -2, 0). 179. -4. 180. Д(0; -2; 0). 181. К(- ^; 4; 0). 183. Щ-1; 7; -2).
184. Возможно. 185. Равно; нет. 186. (1; 3; 3). 187. (6; -4; -3). 188. (-3; 2; -б). 189. Уи; Ш: 190. х = ±3. 191.. а (6; -3; 3) или а (-6; 3; -3). 193. (10; -2; 6).

| с | с | |
| А | ||
| с* С | а а | |
| а | а и. | |
| а | а | |
| с | а | |
| (1 | с | |
| й | а | |
| с | ь | |
| Ь | а |

| . 1) (10; -4; 7); 2) (-2; 3; -4). 200. (10; -4; 6), |
194. 0(0; 0; 0). 195. в) б. 196. АС.
5-,---16.201.(11,-2,-13). 202.
| , /370. 2ОЗ.в = |; /и = 9. о 2 |
/70. 2ОЗ.в = |;
204. 1) 5 + 55; 2) 5-56. 205. 1) \а\ 2) \а. 207. 1) Ь-а; 2) 2Ь-а; 3) 6--*а.
218}. 1) 90'; 2) 50°; 3) 140°. 211. 1) 0; 2) -12. 212. 1)д,- 2) -1. 213. 46°. 215. 150. 216. созС =•/]§. 217..ОО = |(зй + 5 + г). 210. 60°. 220. а,Ь— стороны ромба. 230. 145 м. 282. АВ+^ВС. 235. 1) р; 2) ]? + д; 3) д+р-^г; 4) ^Р + Я+^г. 286. 1) ОМ=^а+^с; 2) 05 = а + с-|,- 3) <Ж=й+*(с-&). 237. 1)(-2; -1; -5);
| | |
| 4); (~3;б; |
~--;^;-1|; 2) (-3;
| 240. |
| м/с. |
= ^?. 241.
ч - - ,' °
| 35Н. |
242. 42 «, 73,2 Н; -, 4|к. «35 Н. 248. 15^3 «26; ЗоУз - 52,0.244.
245. Больше во втором сл^'чае. 246.45°. 247. * -^Ы1й22 - (41 + й|)2 ■ 8.т2ср. 248. ■ 7о(а^2б).
| искомое 2) =14,8 Ц*,8Щ |. |
Указание: рассмотреть систему Л ^ _. с^„2х' где чеРез ^ обозначено
расстояние. 249. 1) 36 см; 2) ЛЕ-,;."!'.. 250. =9,17 см. 251. 1) =16,4 см;
га + га т + л
см. 252. 60°. -253. агссоз4- «54°44'. 254. агссоз
| 5Г48'. 255. |
■уз
| 22о |
| 256. 1) 45°; 2)30°, 30°. |
Ответы к тестам
| Т-3.1 |
| ■Т-3.2 |
| а | е |
| е | а |
| а | а |
| а | а |
| & | а |
| е | а |
| Ь | с |
| е | е |
| с | с |
| а | Ь |
Т-2.2
Date: 2015-04-23; view: 1457; Нарушение авторских прав