
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

СЛЕДСТВИЯ. естественно-математического направления
|
|
ГЕОМЕТРИЯ

|

 Учебник для 10 классов
Учебник для 10 классов
естественно-математического направления
общеобразовательных школ
 Утверждено Министерством образования и науки Республики Казахстан
Утверждено Министерством образования и науки Республики Казахстан
I \
Алматы "Мектеп"700Б""
 |
| I8ВN 9965-33—755-1 |
Условные обозначения:
* — задачи средней сложности;
■ задачи повышенной сложности; — задания внутри параграфа;
] — материал необязателен для обучения в классах естественно-математического направления общеобразовательных школ.
Кайдасов Ж. и др.
К15 Геометрия. Учебник для 10 классов естественно-математического направления общеобразовательных школ / Ж. Кайдасов, В. Гусев, А, Кагазбаева. — Алматы: Издательство "Мектеп", 2006. — 88 с.
1ВВЫ 9965—33-755—1
В
ББК 22.151я72
© Кайдасов Ж., Гусев В., Кагазбаева А., 2006
© Садвакасов А,, оформление обложки, 2006
© Издательство "Мектеп", художественное оформление, 2006
Все права защищены Имущественные права на издание принадлежат издательству "Мектеп"
| ББК 22.151я72 К15 |
| * * — |
ВВЕДЕНИЕ
Ребята, в предыдущих классах вы изучали геометрию на плоскости — планиметрию, Теперь зам предстоит углубить свои знания, изучая геометрию в пространстве, т.е. стереометрию.
Изучение геометрических фигур дает возможность понять свойства различных предметов в окружающем нас мире более углубленно, а также научиться применять их на практике.
Курс геометрии для 10 классов изложен в четырех главах. В I главе приведены аксиомы пространства и доказаны вытекающие из них следствия. II и III главы содержат основной материал, обязательный для учащихся 10 классов. Он предназначен для изучения перпендикулярности и параллельности прямых и плоскостей.
В IV главе, в которой говорится о координатах и векторах, рассматриваются методы геометрии, разработанные позднее. Эта глава особенно полезна для учащихся, которые желают продолжить углубленное изучение математики.
Главы разделены на параграфы. В конце каждого параграфа для повторения и закрепления теоретического материала даны вопросы, задания и задачи. Предложенные задачи подразделяются на три уровня: А — уровень, обязательный для каждого ученика; В — средний уровень; С — уровень, выбираемый по желанию учащегося.
В конце II—-IV глав приведены тестовые задания для проверки уровня знаний. Условия тестовых заданий изложены в виде математических символов и чертежей.
По сложности задания ориентированы на обязательный или средний уровень знаний.
При чтении теоретического материала следует обратить особое внимание на выделенные слова. Объясняя смысл выделенных курсивом геометрических терминов и понятий, необходимо приводить примеры. Полужирным шрифтом обозначены самые важные утверждения. Поняв их, нужно уметь доказывать и применять в решении задач.
Важное место в полном усвоении учебного материала занимают чертежи, которые необходимы для лучшего понимания сути изложенного теоретического материала. Глубокое их усвоение, конечно, потребует немало усидчивости и терпения;
Геометрия как часть царицы наук — математики — возникла в глубокой древности, что было обусловлено практической потребностью измерения земельных участков, объемов и др. Она является важнейшим орудием в изучении природы, плодотворно применяется в различных областях не только математики, но и других наук, в практической деятельности людей. Изучение геометрии открывает перед вами удивительную возможность постижения окружающего нас мира.
Глава I. АКСИОМЫ СТЕРЕОМЕТРИИ И ИХ ПРОСТЕЙШИЕ
СЛЕДСТВИЯ
§1. АКСИОМЫ СТЕРЕОМЕТРИИ
В разделе планиметрии элементарной геометрии вы изучали свойства геометрических фигур, лежащих в одной плоскости. Теперь мы приступаем к изучению свойств фигур, у которых не все точки лежат в одной плоскости, т.е. фигур пространства. Эта часть геометрии называется стереометрией.
Стереометрия (от греч. згегеоз — пространственный и теггео — измеряю)—раздел геометрии, исследующий свойства пространственных фигур. В стереометрии рассматриваются математические модели тех материальных объектов, с которыми ежедневно имеют дело архитекторы, конструкторы, строители и другие специалисты. Кроме того, школьный курс стереометрии служит основой черчения и начертательной геометрии — важнейших дисциплин любого технического вуза, поэтому этот раздел геометрии необходим всем.
Основными фигурами в пространстве являются точка, прямая и плоскость. Они принимаются без определений.
Как вы помните, в планиметрии рассматривалась только одна плоскость, и все изучаемые фигуры располагались в этой единственной плоскости. В стереометрии же приходится различать много плоскостей. Будем считать, что законы планиметрии распространяются на каждую плоскость.
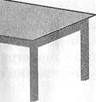
Материальными моделями части плоскости являются, например, поверхность оконного стекла, хорошо отполированного пола и т.п. (рис. 1,а). Понятно, что это грубые модели. В геометрии плоскость мыслится неограниченной, идеально ровной и гладкой, не имеющей толщины.
Изображают плоскости в виде параллелограммов или других ограниченных частей плоскости (рис. 1,б,в). Обозначают их обычно греческими буквами а, р, у, 8 и др. Точки же и прямые отмечают так же, как в планиметрии.
|

|
б)
в)
Рис. 1
Введение нового геометрического образа — плоскости—заставляет расширить систему аксиом. Поэтому мы вводим группу аксиом С, которая выражает основные свойства плоскостей в пространстве. Эта группа состоит из следующих аксиом.
Date: 2015-04-23; view: 1196; Нарушение авторских прав